Aller au contenu

Les sujets de la banque pour les premières, et les annales pour les Term !

Première

Tous les sujets QCM de la banque officielle sont ici :

1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 12 - 13 - 14 - 15 - 16 - 17 - 18 - 19 - 20 - 21 - 22 - 24 - 25 - 26 - 27 - 28 - 29 - 30 - 31 - 32 - 33 - 34 - 35 - 36 - 37 - 38 - 39 - 40 - 41 - 42 - 43 - 44 - 45 - 46 - 47 - 48 - 49 - 50 - 51 - 52 - 53 - 54 - 55 - 56 - 57 - 58 - 59 - 60 - 61 - 62 - 63 - 64 - 65 - 66 - 67 - 68 - 69 - 70 - 71 - 72 - 73 - 74 - 75 - 76 - 77 - 78 - 79 - 80 - 81 - 82 - 83 - 84 - 85 - 86 - 87 - 88 - 89 - 90 - 91 - 92 - 93 - 94 - 95 - 96 - 97 - 98 - 99 - 100 - 101 - 102 - 103 - 104 - 105 - 106 - 107 - 108 - 109 - 110 - 111 - 112 - 113 - 114 - 115 - 116 - 117 - 118 - 119 - 120 - 121 - 122 - 123 - 124 - 125 - 126 - 127 - 128 - 129 - 130 - 131 - 132 - 133 - 134 - 137 - 138 - 139 - 140 - 141 - 142 - 143 - 144 - 145 - 146 - 147 - 148 - 149 - 150 - 151 - 152 - 153 - 154 - 156 - 157 - 158 - 159 - 160 - 161 - 162 - 163 - 164 - 165 - 166 - 167 - 168 - 169 - 170 - 171 - 172 - 173 - 174 - 175 - 176 - 177 - 178 - 179 - 180 - 181 - 182 - 183 - 184 - 185 - 187 - 188 - 189 - 190 - 191 - 192 - 193 - 194 - 195 - 196 - 197 - 198 - 199 - 200 - 201 - 202 - 203 - 204 - 205 - 206 - 207 - 208 - 209 - 210 - 211 - 212 - 213 - 214 - 215 - 216 - 217 - 218 - 219 - 220 - 221 - 222 - 223 - 224 - 225 - 226 - 227 - 228 - 230 - 231 - 232 - 233 - 234 - 235 - 236 - 237 - 238 - 239 - 240 - 241 - 242 - 243 - 244 - 245 - 246 - 247 - 249 - 250 - 251 - 252 - 253 - 254 - 255 - 256 - 257 - 258 - 259 - 260 - 261 - 262 - 263 - 264 - 265 - 266 - 267 - 268 - 269

Terminale

A noter

A partir de 2023, vous ne pouvez plus choisir 3 des 5 exercices comme auparavant : les 3 exercices sont maintenant imposés.

Sujets Corrigé Contenus
2024 - Sujet Zéro-A Ex 1 [6 points] : (Réseau et architecture 1re ) (Protocoles Tle) Architecture matérielle, réseaux, routeurs et protocoles de routage.
Ex 2 [6 points] : (Algorithmique, Dictionnaires, Listes 1re) Listes, dictionnaires et programmation de base en Python.
Ex 3 [8 points] : (Arbres, Graphes, BDD, SQL Tle) Graphes, algorithmes sur les graphes, bases de données et requêtes SQL.
2024 - Sujet Zéro-B Ex 1 [6 points] : (Récursivité, listes, prog Dynamique Tle) Notion de listes, récursivité et programmation dynamique
Ex 2 [6 points] : (UNIX, SE, Piles et Files Tle) Systèmes d’exploitation, commandes UNIX, structures de données (de type LIFO et FIFO) et processus
Ex 3 [8 points] : (Dictionnaires, POO, BDD et SQL Tle) Programmation Python (dictionnaire), Programmation orientée objet, bases de données relationnelles et requêtes SQL.
2024 - Etranger - jour 1 Ex 1 [6 points] : Programmation dynamique, Graphes, réseaux
Ex 2 [6 points] : Réseaux (1re) et protocoles de routage
Ex 3 [8 points] : POO, Bases de données et SQL
2024 - Etranger - jour 2 Ex 1 [6 points] : Python en général, programmation orientée objet et récursivité.
Ex 2 [6 points] : programmation objet, récursivité, arbres binaires et systèmes d’exploitation (1re).
Ex 3 [8 points] : codage binaire (1re), bases de données relationnelles et requêtes SQL.
2024 - Amérique Nord - Sujet 1 Ex 1 [6 points] : POO, File, Ordonnancement et Interblocage
Ex 2 [6 points] : Graphes
Ex 3 [8 points] : Python, Bases de Données, SQL
2024 - Amérique Nord - Sujet 2 Ex 1 [6 points] : Algo de Tri, Programmation, récursivité (Erreur dans l'exercice avec beaucoup d'imprécisions)
Ex 2 [6 points] : SQL, BDD<brEx 3 [8 points] : POO, Structures de données, réseaux et architecture
2024 - Asie Sujet 1 Ex 1 [6 points] : la programmation Python, la programmation orientée objet et l’algorithmique
Ex 2 [6 points] : graphes, programmation, structure de pile et algorithmique des graphes.
Ex 3 [8 points] : programmation Python, programmation orientée objet, bases de données relationnelles et requêtes SQL.
2024 - Asie Sujet 2 Ex 1 [6 points] : la programmation Python (listes, dictionnaires 1re) et la méthode “diviser pour régner”.
Ex 2 [6 points] : programmation orientée objet et structures de données linéaires.
Ex 3 [8 points] : bases de données relationnelles, requêtes SQL et programmation en Python.
2024 - Métropole Sujet 1 Ex 1 [6 points] : la programmation objet en Python et les graphes.
Ex 2 [6 points] : protocoles de routage, de sécurité des communications et de base de données relationnelle.
Ex 3 [8 points] : programmation orientée objet sur les arbres binaires de recherche et récursivité.
2024 - Métropole Sujet 2 Ex 1 [6 points] : bases de données relationnelles, langage SQL et protocoles de sécurisation.
Ex 2 [6 points] : programmation orientée objets, tris, algorithmes gloutons, récursivité et assertions
Ex 3 [8 points] : programmation orientée objet, graphes et utilise la structure de données dictionnaire.
2024 - Polynésie Sujet 1 Ex 1 [6 points] : graphes et protocoles réseau.
Ex 2 [6 points] : récursivité.
Ex 3 [8 points] : programmation Python (dictionnaire), bases de données relationnelles et requêtes SQL.
2024 - Polynésie Sujet 2 Ex 1 [6 points] : structures de données FILE et PILE, graphes et algorithmes de parcours.
Ex 2 [6 points] : arbres binaires de recherche, POO et récursivité
Ex 3 [8 points] : protocoles réseau, bases de données relationnelles et requêtes SQL, algorithmique et programmation en Python.
2024 - Suède Ex 1 [6 points] : listes de listes, programmation orientée objet.
Ex 2 [6 points] : architecture réseaux, routage.
Ex 3 [8 points] : programmation Python, traitement de données en table et bases de données relationnelles.
2023 - Etranger - jour 1 Ex 1 [3 points] : Bases de données relationnelles et le langage SQL
Ex 2 [3 points] : Réseaux et protocoles de routage
Ex 3 [6 points] : Structures de données files
2023 - Etranger - jour 2 Ex 1 [4 points] : Adressage IP et protocoles de routage
Ex 2 [4 points] : Bases de données relationnelles et langage SQL
Ex 3 [4 points] : programmation en Python, manipulation des chaines de caractères, arbres binaires de recherche et parcours de liste
2023 - Liban - jour 1 Ex 1 [3 points] : Algorithmique et programmation
Ex 2 [5 points] : Bases de données, représentation des données et réseaux
Ex 3 [4 points] : Piles, arbres et algorithmique
2023 - Réunion - jour 1 Ex 1 [4 points] : Réseaux et protocoles de routage
Ex 2 [4 points] : Programmation orientée objet et dictionnaires
Ex 3 [4 points] : Bases de données relationnelles et langage SQL
2023 - Métropole - jour 1 Ex 1 [3 points] : Base de données relationnelles et le langage SQL
Ex 2 [3 points] : Réseaux
Ex 3 [6 points] : Programmation orientée objet en Python et algorithmique
2023 - Polynésie - jour 1 Ex 1 [4 points] : Bases de données relationnelles et le langage SQL
Ex 2 [3 points] : * Gestions des processus et programmation orientée objet*
Ex 3 [5 points] : Algorithmique, programmation orientée objet et méthode diviser pour régner
2023 - Liban - jour 2 Ex 1 [4 points] : Bases de données
Ex 2 [3 points] : Réseaux, programmation Python et algorithmique
Ex 3 [5 points] : Arbres et algorithmique
2023 - Réunion - jour 2 Ex 1 [4 points] : Arbres binaires de recherche, programmation orientée objet et récursivité
Ex 2 [4 points] : Réseaux et protocoles de routage
Ex 3 [4 points] : Bases de données relationnelles et langage SQL
2023 - Métropole - jour 2 Ex 1 [3 points] : Protocoles Réseaux
Ex 2 [3 points] : Bases de données et langage SQL
Ex 3 [6 points] : Arbres binaires, files et programmation orientée objet
2023 - Polynésie - jour 2 Ex 1 [4 points] : Arbres binaires de recherche, programmation orientée objet et récursivité
Ex 2 [4 points] : Bases de données, modèle relationnel et langage SQL
Ex 3 [4 points] : Architecture matérielle, processus et ordonnancement
2023 - Sujet Zéro-A Ex 1 [3 points] : bases de données et types construits de données
Ex 2 [3 points] : architecture matérielle, réseaux et systèmes d'exploitation
Ex 3 [6 points] : arbres binaires de recherche et programmation objet
2023 - Sujet Zéro-B Ex 1 [4 points] : ligne de commande sous Linux, traitement de données en tables et bases de données
Ex 2 [4 points] : analyse et écriture de programmes récursifs
Ex 3 [4 points] : arbres binaires de recherche et notion d'objet
2022 - Amérique du Nord - Jour 1 Ex 1 : bases de données (Vacances autrement)
Ex 2 : réseaux, protocoles de routage
Ex 3 : arbres binaires de recherche, algorithmique
Ex 4 : chaîne de caractère, tableau, Python
Ex 5 : files, tableaux, algorithmique
2022 - Amérique du Nord - Jour 2 Ex 1 : liste, arbres binaires de recherche, POO
Ex 2 : systèmes d'exploitation, processus
Ex 3 : bases de données (site web salle de cinéma)
Ex 4 : arbres binaires, algorithmique
Ex 5 : tableaux à deux dimensions, Python
2022 - Amérique du Sud - Jour 1 Ex 1 : bases de données (maternité)
Ex 2 : programmation, algorithmes de tri
Ex 3 : arbres binaires
Ex 4 : systèmes d'exploitation, processus
Ex 5 : réseaux, protocoles de routage
2022 - Amérique du Sud Jour 2 Ex 1 : programmation, algorithmique, complexité
Ex 2 : réseaux, protocoles de routage
Ex 3 : bases de données (vente vélos électriques)
Ex 4 : Python, récursivité, diviser pour régner
Ex 5 : arbres binaires, POO, récursivité
2022 - Asie - Jour 1 Ex 1 : algorithmique, chaînes de caractères, complexité
Ex 2 : bases de données (restaurant site de réservation)
Ex 3 : systèmes d'exploitation, Linux
Ex 4 : POO, Python
Ex 5 : Python
2022 - Asie - Jour 2 Ex 1 : système d'exploitation Linux
Ex 2 : arbres binaires de recherche
Ex 3 : structures de donnée, programmation (jeu de la vie)
Ex 4 : bases de données (club de tennis)
Ex 5 : exécution de programmes, recherche et correction de bugs
2022 - Centres étrangers - Jour 1 Ex 1 : structures de données, listes, p-uplets, dictionnaires
Ex 2 : structures de données, files, POO, Python
Ex 3 : structures de données, dictionnaires
Ex 4 : bases de données (centre météorologique)
Ex 5 : architectures matérielles, réseaux, protocoles de routage
2022 - Centres étrangers - Jour 2 Ex 1 : Python, récursivité
Ex 2 : structures de données, dictionnaires, Python
Ex 3 : bases de données (enseignants, évaluations)
Ex 4 : structures de données, POO, Python
Ex 5 : architectures matérielles, systèmes d'exploitation, réseaux
2022 - Mayotte - Jour 1 Ex 1 : structures de données, listes, piles, files
Ex 2 : structures de données, POO, Python
Ex 3 : bases de données (QCM NSI)
Ex 4 : algorithmique, arbres binaires
Ex 5 : réseau, protocole de routage
2022 - Mayotte - Jour 2 Ex 1 : structures de données, piles
Ex 2 : bases de données (hôtel)
Ex 3 : binaire, systèmes d'exploitation
Ex 4 : arbres binaires de recherche
Ex 5 : algorithmes, Python (TAKAZU)
2022 - Polynésie - Jour 2 Ex 1 : programmation, récursivité, Python
Ex 2 : architecture matérielle, ordonnancement, booléens
Ex 3 : bases de données (site web)
Ex 4 : structures de données, piles
Ex 5 : algorithmique, arbres binaires
2022 - Métropole septembre Ex 1 : protocoles de communication, réseaux, protocoles de routage
Ex 2 : tableaux, dictionnaires, Python
Ex 3 : bases de données (tableau périodique)
Ex 4 : piles, POO, Python
Ex 5 : traitement des données en tables, Python
2022 - Métropole - Jour 1 Ex 1 : structures de données
Ex 2 : bases de données (cinéma)
Ex 3 : binaire, routage
Ex 4 : arbres binaires, diviser pour régner, récursivité
Ex 5 : POO
2022 - Métropole - Jour 2 Ex 1 : arbres binaires de recherche, POO, récursivité
Ex 2 : structures de données (piles)
Ex 3 : réseaux, routage
Ex 4 : bases de données (musique)
Ex 5 : POO, diviser pour régner
2021 - Centres étrangers - Jour 1 Ex 1 : POO (codage César)
Ex 2 : dictionnaires, Python (vélos en location)
Ex 3 : arbres binaires de recherche
Ex 4 : réseaux, masque de sous-réseau, conversion décimal/binaire, Python
Ex 5 : piles, Python
2021 - Centres étrangers - Jour 2 Ex 1 : piles, Python (mélange d'une liste)
Ex 2 : tuples, listes, Python (labyrinthe)
Ex 3 : conversion décimal/binaire, table de vérité, codage des caractères (cryptage avec XOR)
Ex 4 : bases de données (club de handball)
Ex 5 : POO (bandeau à LED)
2021 - Amérique du Nord Ex 1 : bases de données (parc informatique)
Ex 2 : routage, processus, SOC (constructeur automobile)
Ex 3 : tableaux, Python (calcul de réductions)
Ex 4 : arbres binaires (compétition de badminton)
Ex 5 : piles, files, Python
2021 - Métropole Libres - Jour 1 Ex 1 : bases de données (théâtre)
Ex 2 : piles, POO, Python
Ex 3 : processus, RIP, OSPF
Ex 4 : tableaux, Python (labyrinthe)
Ex 5 : tableaux, récursivité, diviser pour régner (inversions dans un tableau)
2021 - Métropole Libres - Jour 2 Ex 1 : bases de données (bibliothèque)
Ex 2 : processus
Ex 3 : arbres binaires de recherche, POO
Ex 4 : récursivité, Python (mélange d'une liste)
Ex 5 : tableaux, Python
2021 - Métropole - Jour 1 Ex 1 : arbres binaires de recherche, POO
Ex 2 : processus, opérateurs booléens
Ex 3 : bases de données (trains)
Ex 4 : tri fusion, diviser pour régner, Python
Ex 5 : réseaux, protocoles de routage
2021 - Métropole - Jour 2 Ex 1 : arbres, POO
Ex 2 : bases de données (restaurant)
Ex 3 : réseaux, protocoles de routage
Ex 4 : systèmes d'exploitation, processus
Ex 5 : files, Python
2021 - Métropole Septembre Sujet 1 Ex 1 : protocoles de communication, architecture réseau, routage
Ex 2 : recherche dichotomique, récursivité
Ex 3 : bases de données (AirOne)
Ex 4 : programmation objet, spécification
Ex 5 : arbre, arbre binaire, pile, Python
2021 - Métropole Septembre Sujet 2 Ex 1 : protocoles de communication, réseaux, protocoles de routage
Ex 2 : tableaux, dictionnaires, Python
Ex 3 : bases de données (tableau périodique)
Ex 4 : piles, POO, Python
Ex 5 : traitement des données en tables, Python
2021 - Polynésie Sujet 2 Ex 1 : algorithmes de tri, Python
Ex 2 : bases de données (vente en ligne)
Ex 3 : arbres binaires de recherche, POO
Ex 4 : architectures matérielles, systèmes d'exploitation, routage
Ex 5 : bases de données (vidéo à la demande)
2021 - Sujet Zéro Ex 1 : piles, Python
Ex 2 : récursivité, Python (chemin dans un tableau)
Ex 3 : arbres binaires, arbres binaire de recherche, Python
Ex 4 : bases de données (lycée)
Ex 5 : réseaux, RIP, OSPF (routeurs)

Pas pour les candidat·e·s libres

Exercice 01.1

Programmer la fonction verifie qui prend en paramètre un tableau de valeurs numériques non vide et qui renvoie True si ce tableau est trié dans l’ordre croissant, False sinon.

Exemples :

Exemples :
>>> verifie([0, 5, 8, 8, 9])
True
>>> verifie([8, 12, 4])
False
>>> verifie([-1, 4])
True
>>> verifie([5])
True

1
2
3
4
5
def verifie(tab):
    for i in range(1, len(tab)):
        if tab[i] < tab[i-1]:
            return False
    return True

➡ Rédigez votre code sur Basthon

Exercice 01.2

Les résultats d'un vote ayant trois issues possibles 'A', 'B' et 'C' sont stockés dans un tableau.

Exemple :

urne = ['A', 'A', 'A', 'B', 'C', 'B', 'C', 'B', 'C', 'B']

La fonction depouille doit permettre de compter le nombre de votes exprimés pour chaque artiste. Elle prend en paramètre un tableau et renvoie le résultat dans un dictionnaire dont les clés sont les noms des artistes et les valeurs le nombre de votes en leur faveur.

La fonction vainqueur doit désigner le nom du ou des gagnants. Elle prend en paramètre un dictionnaire dont la structure est celle du dictionnaire renvoyé par la fonction depouille et renvoie un tableau. Ce tableau peut donc contenir plusieurs éléments s’il y a des artistes ex- aequo. Compléter les fonctions depouille et vainqueur ci-après pour qu’elles renvoient les résultats attendus.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
urne = ['A', 'A', 'A','B', 'C', 'B', 'C','B', 'C', 'B']

def depouille(urne):
    resultat = ...
    for bulletin in urne:
        if ...:
            resultat[bulletin] = resultat[bulletin] + 1
        else:
            ...
    return resultat

def vainqueur(election):
    vainqueur = ''
    nmax = 0
    for candidat in election:
        if ... > ... :
            nmax = ...
            vainqueur = candidat
    liste_finale = [nom for nom in election if election[nom] == ...]
    return ...

Exemples d’utilisation :

>>> election = depouille(urne)
>>> election
{'A': 3, 'B': 4, 'C': 3}
>>> vainqueur(election)
['B']

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
urne = ['A', 'A', 'A', 'B', 'C', 'B', 'C', 'B', 'C', 'B']

def depouille(urne):
    resultat = {}
    for bulletin in urne:
        if bulletin in resultat:
            resultat[bulletin] = resultat[bulletin] + 1
        else:
            resultat[bulletin] = 1
    return resultat

def vainqueur(election):
    vainqueur = '' #(1)
    nmax = 0
    for candidat in election:
        if election[candidat] > nmax :
            nmax = election[candidat]
            vainqueur = candidat #(2)
    liste_finale = [nom for nom in election if election[nom] == nmax]
    return liste_finale
  1. Il est pourtant très déconseillé de nommer une variable avec le même nom que la fonction qui la contient...
  2. Cette variable vainqueur est inutile, on ne s'en sert pas dans l'élaboration de la liste finale.

➡ Complétez le code sur Basthon

Exercice 02.1

Écrire une fonction indices_maxi qui prend en paramètre une liste tab, non vide, de nombres entiers et renvoie un couple donnant d’une part le plus grand élément de cette liste et d’autre part la liste des indices de la liste tab où apparaît ce plus grand élément.

Exemple : 

>>> indices_maxi([1, 5, 6, 9, 1, 2, 3, 7, 9, 8])
(9, [3, 8])
>>> indices_maxi([7])
(7, [0])


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
def indices_maxi(tab):
    val_max = tab[0]
    ind_max = []
    for i in range(len(tab)):
        if tab[i] > val_max:
            val_max = tab[i]
    for i in range(len(tab)):
        if tab[i] == val_max:
            ind_max.append(i)
    return (val_max, ind_max)

➡ Rédigez votre code sur Basthon

Exercice 02.2

Cet exercice utilise des piles qui seront représentées en Python par des listes (type list).

On rappelle que l’expression liste_1 = list(liste) fait une copie de listeindépendante de liste, que l’expression x = liste.pop() enlève le sommet de la pile liste et le place dans la variable x et, enfin, que l’expression liste.append(v) place la valeur v au sommet de la pile liste.

Compléter le code Python de la fonction positif ci-dessous qui prend une pile liste de nombres entiers en paramètre et qui renvoie la pile des entiers positifs dans le même ordre, sans modifier la variable liste.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
def positif(pile):
    pile_1 = ...(pile)
    pile_2 = ...
    while pile_1 != []:
        x = ...
        if ... >= 0:
            pile_2.append(...)
    while pile_2 != ...:
        x = pile_2.pop()
        ...
    return pile_1

Exemple : 

>>> positif([-1, 0, 5, -3, 4, -6, 10, 9, -8])
[0, 5, 4, 10, 9]
>>> positif([-2])
[]


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
def positif(pile):
    pile_1 = list(pile)
    pile_2 = []
    while pile_1 != []:
        x = pile_1.pop()
        if x >= 0:
            pile_2.append(x)
    while pile_2 != []:
        x = pile_2.pop()
        pile_1.append(x)
    return pile_1

➡ Complétez le code sur Basthon

Exercice 03.1

Dans cet exercice, les nombres sont des entiers ou des flottants.

Écrire une fonction moyenne renvoyant la moyenne pondérée d’une liste non vide, passée en paramètre, de tuples à deux éléments de la forme (valeur, coefficient) où valeur et coefficient sont des nombres positifs ou nuls. Si la somme des coefficients est nulle, la fonction renvoie None, si la somme des coefficients est non nulle, la fonction renvoie, sous forme de flottant, la moyenne des valeurs affectées de leur coefficient.

Exemple : 

>>> moyenne([(8, 2), (12, 0), (13.5, 1), (5, 0.5)])
9.142857142857142
>>> moyenne([(3, 0), (5, 0)])
None

Dans le premier exemple la moyenne est calculée par la formule :

\(\dfrac{8 \times 2 + 12 \times 0 + 13,5 \times 1 + 5 \times 0,5}{2+0+1+0,5}\)

1
2
3
4
5
6
7
8
9
def moyenne(tab):
    somme = 0
    coeffs = 0
    for couple in tab:
        somme += couple[0] * couple[1]
        coeffs += couple[1]
    if coeffs == 0:
        return None
    return somme / coeffs

➡ Rédigez votre code sur Basthon

Exercice 03.2

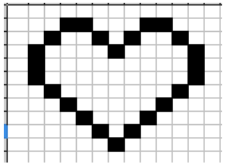image On travaille sur des dessins en noir et blanc obtenu à partir de pixels noirs et blancs : La figure « cœur » ci-dessus va servir d’exemple. On la représente par une grille de nombres, c’est-à-dire par une liste composée de sous-listes de même longueurs. Chaque sous-liste représentera donc une ligne du dessin.

Dans le code ci-dessous, la fonction affiche permet d’afficher le dessin. Les pixels noirs (1 dans la grille) seront représentés par le caractère "*" et les blancs (0 dans la grille) par deux espaces.

La fonction zoomListe prend en argument une liste liste_depart et un entier k. Elle renvoie une liste où chaque élément de liste_depart est dupliqué k fois.

La fonction zoomDessin prend en argument la grille dessin et renvoie une grille où toutes les lignes de dessin sont zoomées k fois et répétées k fois.

Soit le code ci-dessous :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
coeur = [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], \
        [0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0], \
        [0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0], \
        [0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0], \
        [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0], \
        [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0], \
        [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], \
        [0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0], \
        [0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0], \
        [0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0], \
        [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0], \
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]

def affiche(dessin):
    ''' affichage d'une grille : les 1 sont représentés par 
        des " *" , les 0 par deux espaces "  " '''
    for ligne in dessin:
        for col in ligne:
            if col == 1:
                print(" *", end="")
            else:
                print("  ", end="")
        print()


def zoomListe(liste_depart,k):
    '''renvoie une liste contenant k fois chaque 
    élément de liste_depart'''
    liste_zoom = ...
    for elt in ... :
        for i in range(k):
            ...
    return liste_zoom

def zoomDessin(grille,k):
    '''renvoie une grille où les lignes sont zoomées k fois 
    ET répétées k fois'''
    grille_zoom=[]
    for elt in grille:
        liste_zoom = ...
        for i in range(k):
            ... .append(...)
    return grille_zoom

Résultats à obtenir :

>>> affiche(coeur)
image

>>> affiche(zoomDessin(coeur,3))

            * * * * * *                   * * * * * *                  
            * * * * * *                   * * * * * *                  
            * * * * * *                   * * * * * *                  
      * * *             * * *       * * *             * * *            
      * * *             * * *       * * *             * * *            
      * * *             * * *       * * *             * * *            
* * *                         * * *                         * * *      
* * *                         * * *                         * * *      
* * *                         * * *                         * * *      
* * *                                                       * * *      
* * *                                                       * * *      
* * *                                                       * * *      
* * *                                                       * * *      
* * *                                                       * * *      
* * *                                                       * * *      
      * * *                                           * * *            
      * * *                                           * * *            
      * * *                                           * * *            
            * * *                               * * *                  
            * * *                               * * *                  
            * * *                               * * *                  
                  * * *                   * * *                        
                  * * *                   * * *                        
                  * * *                   * * *                        
                        * * *       * * *                              
                        * * *       * * *                              
                        * * *       * * *                              
                              * * *                                    
                              * * *                                    
                              * * *

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
coeur = [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], \
        [0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0], \
        [0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0], \
        [0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0], \
        [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0], \
        [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0], \
        [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], \
        [0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0], \
        [0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0], \
        [0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0], \
        [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0], \
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]

def affiche(dessin):
    ''' affichage d'une grille : les 1 sont représentés par 
    des " *" , les 0 par deux espaces "  " '''
    for ligne in dessin:
        for col in ligne:
            if col == 1:
                print(' *',end='')
            else:
                print('  ',end='')
        print()


def zoomListe(liste_depart, k):
    '''renvoie une liste contenant k fois chaque 
    élément de liste_depart'''
    liste_zoom = []
    for elt in liste_depart:
        for i in range(k):
            liste_zoom.append(elt)
    return liste_zoom

def zoomDessin(grille, k):
    '''renvoie une grille où les lignes sont zoomées k fois 
    ET répétées k fois'''
    grille_zoom = []
    for elt in grille:
        liste_zoom = zoomListe(elt, k)
        for i in range(k):
            grille_zoom.append(liste_zoom)
    return grille_zoom

➡ Complétez le code sur Basthon

Exercice 04.1

Écrire une fonction a_doublon qui prend en paramètre une liste triée de nombres et renvoie True si la liste contient au moins deux nombres identiques, False sinon.

Par exemple :

>>> a_doublon([])
False
>>> a_doublon([1])
False
>>> a_doublon([1, 2, 4, 6, 6])
True
>>> a_doublon([2, 5, 7, 7, 7, 9])
True
>>> a_doublon([0, 2, 3])
False

1
2
3
4
5
def a_doublon(lst):
    for i in range(len(lst)-1):
        if lst[i] == lst[i+1]:
            return True
    return False

➡ Rédigez votre code sur Basthon

Exercice 04.2

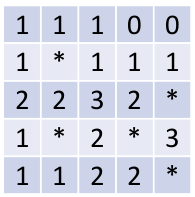
On souhaite générer des grilles du jeu de démineur à partir de la position des bombes à placer.
On se limite à la génération de grilles carrées de taille \(n \times n\) où \(n\) est le nombre de bombes du jeu.

Dans le jeu du démineur, chaque case de la grille contient soit une bombe, soit une valeur qui correspond aux nombres de bombes situées dans le voisinage direct de la case (au- dessus, en dessous, à droite, à gauche ou en diagonale : chaque case a donc 8 voisins si elle n'est pas située au bord de la grille).

Voici un exemple de grille \(5 \times 5\) de démineur dans laquelle la bombe est représentée par une étoile :

image

On utilise une liste de listes pour représenter la grille et on choisit de coder une bombe par la valeur -1.

L'exemple ci-contre sera donc codé par la liste :

[[1, 1, 1, 0, 0],
[1, -1, 1, 1, 1],
[2, 2, 3, 2, -1],
[1, -1, 2, -1, 3],
[1, 1, 2, 2, -1]]

Compléter le code suivant afin de générer des grilles de démineur, on pourra vérifier que l’instruction genere_grille([(1, 1), (2, 4), (3, 1), (3, 3), (4, 4)]) produit bien la liste donnée en exemple.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def voisinage(n, ligne, colonne):
    """ Renvoie la liste des coordonnées des voisins de la case
    (ligne, colonne) en gérant les cases sur les bords. """
    voisins = []
    for l in range(max(0,ligne-1), min(n, ligne+2)):
        for c in range(max(0, colonne-1), min(n, colonne+2)):
            if (l, c) != (ligne, colonne):
                voisins.append((l,c))
    return voisins


def incremente_voisins(grille, ligne, colonne):
    """ Incrémente de 1 toutes les cases voisines d'une bombe."""
    voisins = ...
    for l, c in voisins:
        if grille[l][c] != ...: # si ce n'est pas une bombe
            ...  # on ajoute 1 à sa valeur



def genere_grille(bombes):
    """ Renvoie une grille de démineur de taille nxn où n est
    le nombre de bombes, en plaçant les bombes à l'aide de
    la liste bombes de coordonnées (tuples) passée en
    paramètre. """
    n = len(bombes)
    # Initialisation d'une grille nxn remplie de 0
    grille = [[0 for colonne in range(n)] for ligne in range(n)]
    # Place les bombes et calcule les valeurs des autres cases
    for ligne, colonne in bombes:
        grille[ligne][colonne] = ... # place la bombe
        ... # incrémente ses voisins

    return grille

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def voisinage(n, ligne, colonne):
    """ Renvoie la liste des coordonnées des voisins de la case
    (ligne, colonne) en gérant les cases sur les bords. """
    voisins = []
    for l in range(max(0,ligne-1), min(n, ligne+2)):
        for c in range(max(0, colonne-1), min(n, colonne+2)):
            if (l, c) != (ligne, colonne):
                voisins.append((l,c))
    return voisins


def incremente_voisins(grille, ligne, colonne):
    """ Incrémente de 1 toutes les cases voisines d'une bombe."""
    voisins = voisinage(len(grille), ligne, colonne)
    for l, c in voisins:
        if grille[l][c] != -1: # si ce n'est pas une bombe
            grille[l][c] += 1  # on ajoute 1 à sa valeur



def genere_grille(bombes):
    """ Renvoie une grille de démineur de taille nxn où n est
    le nombre de bombes, en plaçant les bombes à l'aide de
    la liste bombes de coordonnées (tuples) passée en
    paramètre. """
    n = len(bombes)
    # Initialisation d'une grille nxn remplie de 0
    grille = [[0 for colonne in range(n)] for ligne in range(n)]
    # Place les bombes et calcule les valeurs des autres cases
    for ligne, colonne in bombes:
        grille[ligne][colonne] = -1 # place la bombe
        incremente_voisins(grille, ligne, colonne) # incrémente ses voisins

    return grille

➡ Complétez le code sur Basthon

Exercice 05.1

Écrire en python deux fonctions :

  • lancer de paramètre n, un entier positif, qui renvoie un tableau de type list de n entiers obtenus aléatoirement entre 1 et 6 (1 et 6 inclus) ;

  • paire_6 de paramètre tab, un tableau de type list de n entiers entre 1 et 6 obtenus aléatoirement, qui renvoie un booléen égal à True si le nombre de 6 est supérieur ou égal à 2, False sinon.

On pourra utiliser la fonction randint(a,b) du module random pour laquelle la documentation officielle est la suivante :

Renvoie un entier aléatoire N tel que a <=N <= b.

Exemples :

>>> lancer1 = lancer(5)
[5, 6, 6, 2, 2]
>>> paire_6(lancer1)
True
>>> lancer2 = lancer(5)
[6, 5, 1, 6, 6]
>>> paire_6(lancer2)
True
>>> lancer3 = lancer(3)
[2, 2, 6]
>>> paire_6(lancer3)
False
>>> lancer4 = lancer(0)
[]
>>> paire_6(lancer4)
False

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
from random import randint

def lancer(n):
    return [randint(1,6) for _ in range(n)]

def paire_6(tab):
    nb = 0
    for elt in tab:
        if elt == 6:
            nb += 1
    if nb >=2 :
        return True
    else:
        return False

➡ Rédigez votre code sur Basthon

Exercice 05.2

On considère une image en 256 niveaux de gris que l’on représente par une grille de nombres, c’est-à-dire une liste composée de sous-listes toutes de longueurs identiques.

La largeur de l’image est donc la longueur d’une sous-liste et la hauteur de l’image est le nombre de sous-listes.

Chaque sous-liste représente une ligne de l’image et chaque élément des sous-listes est un entier compris entre 0 et 255, représentant l’intensité lumineuse du pixel.

Le négatif d’une image est l’image constituée des pixels x_n tels que x_n + x_i = 255 où x_i est le pixel correspondant de l’image initiale.

Compléter le programme suivant : 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def nbLig(image):
    '''renvoie le nombre de lignes de l'image'''
    return ...

def nbCol(image):
    '''renvoie la largeur de l'image'''
    return ...

def negatif(image):
    '''renvoie le negatif de l'image sous la forme
       d'une liste de listes'''

    # on cree une image de 0 aux memes dimensions que le parametre image
    L = [[0 for k in range(nbCol(image))] for i in range(nbLig(image))]

    for i in range(nbLig(image)):
        for j in range(...):
            L[i][j] = ...
    return L

def binaire(image, seuil):
    '''renvoie une image binarisee de l'image sous la forme
       d'une liste de listes contenant des 0 si la valeur
       du pixel est strictement inferieure au seuil
       et 1 sinon'''

    # on cree une image de 0 aux memes dimensions que le parametre image
    L = [[0 for k in range(nbCol(image))] for i in range(nbLig(image))]

    for i in range(nbLig(image)):
        for j in range(...):
            if image[i][j] < ... :
                L[i][j] = ...
            else:
                L[i][j] = ...
    return L

Exemples :

>>> img=[[20, 34, 254, 145, 6], [23, 124, 237, 225, 69], [197, 174,
207, 25, 87], [255, 0, 24, 197, 189]]
>>> nbLig(img)
4
>>> nbCol(img)
5
>>> negatif(img)
[[235, 221, 1, 110, 249], [232, 131, 18, 30, 186], [58, 81, 48, 230,
168], [0, 255, 231, 58, 66]]
>>> binaire(img,120)
[[0, 0, 1, 1, 0], [0, 1, 1, 1, 0], [1, 1, 1, 0, 0], [1, 0, 0, 1, 1]]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def nbLig(image):
    '''renvoie le nombre de lignes de l'image'''
    return len(image)

def nbCol(image):
    '''renvoie la largeur de l'image'''
    return len(image[0])

def negatif(image):
    '''renvoie le negatif de l'image sous la forme
       d'une liste de listes'''

    # on cree une image de 0 aux memes dimensions que le parametre image
    L = [[0 for k in range(nbCol(image))] for i in range(nbLig(image))]

    for i in range(nbLig(image)):
        for j in range(nbCol(image)):
            L[i][j] = 255 - image[i][j]
    return L

def binaire(image, seuil):
    '''renvoie une image binarisee de l'image sous la forme
       d'une liste de listes contenant des 0 si la valeur
       du pixel est strictement inferieure au seuil
       et 1 sinon'''

    # on cree une image de 0 aux memes dimensions que le parametre image
    L = [[0 for k in range(nbCol(image))] for i in range(nbLig(image))]

    for i in range(nbLig(image)):
        for j in range(nbCol(image)):
            if image[i][j] < seuil :
                L[i][j] = 0
            else:
                L[i][j] = 1
    return L

➡ Complétez le code sur Basthon

Exercice 06.1

Programmer la fonction recherche, prenant en paramètre un tableau non vide tab (type list) d'entiers et un entier n, et qui renvoie l'indice de la dernière occurrence de l'élément cherché. Si l'élément n'est pas présent, la fonction renvoie la longueur du tableau.

Exemples 

>>> recherche([5, 3],1)
2
>>> recherche([2,4],2)
0
>>> recherche([2,3,5,2,4],2)
3


1
2
3
4
5
6
def recherche(tab, n):
    indice_solution = len(tab)
    for i in range(len(tab)):
        if tab[i] == n:
            indice_solution = i
    return indice_solution

➡ Rédigez votre code sur Basthon

Exercice 06.2

On souhaite programmer une fonction donnant la distance la plus courte entre un point de départ et une liste de points. Les points sont tous à coordonnées entières. Les points sont donnés sous la forme d'un tuple de deux entiers. La liste des points à traiter est donc un tableau de tuples.

On rappelle que la distance entre deux points du plan de coordonnées \((x;y)\) et \((x';y')\) est donnée par la formule :

\[d=\sqrt{(x-x')^2+(y-y')^2}\]

On importe pour cela la fonction racine carrée (sqrt) du module math de Python.

Compléter le code des fonctions distance et plus_courte_distance fournies ci-dessous pour qu’elles répondent à leurs spécifications.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
from math import sqrt     # import de la fonction racine carrée

def distance(point1, point2):
    """ Calcule et renvoie la distance entre deux points. """
    return sqrt((...)**2 + (...)**2)

def plus_courte_distance(tab, depart):
    """ Renvoie le point du tableau tab se trouvant à la plus courte distance du point depart."""
    point = tab[0]
    min_dist = ...
    for i in range (1, ...):
        if distance(tab[i], depart)...:
            point = ...
            min_dist = ...
    return point

Exemples :

>>> distance((1, 0), (5, 3))
5.0
>>> distance((1, 0), (0, 1))
1.4142135623730951
>>> plus_courte_distance([(7, 9), (2, 5), (5, 2)], (0, 0))
(2, 5)
>>> plus_courte_distance([(7, 9), (2, 5), (5, 2)], (5, 2))
(5, 2)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
from math import sqrt

def distance(point1, point2):
    """ Calcule et renvoie la distance entre deux points. """
    return sqrt((point1[0] - point2[0])**2 + ((point1[1] - point2[1]))**2)

def plus_courte_distance(tab, depart):
    """ Renvoie le point du tableau tab se trouvant à la plus courte distance du point depart."""
    point = tab[0]
    min_dist = distance(point, depart)
    for i in range (1, len(tab)):
        if distance(tab[i], depart) < min_dist:
            point = tab[i]
            min_dist = distance(tab[i], depart)
    return point

➡ Complétez le code sur Basthon

Exercice 07.1

Programmer la fonction fusion prenant en paramètres deux tableaux non vides tab1 et tab2 (type list) d'entiers, chacun dans l’ordre croissant, et renvoyant un tableau trié dans l’ordre croissant et contenant l’ensemble des valeurs de tab1 et tab2.

Exemples :

>>> fusion([3, 5], [2, 5])
[2, 3, 5, 5]
>>> fusion([-2, 4], [-3, 5, 10])
[-3, -2, 4, 5, 10]
>>> fusion([4], [2, 6])
[2, 4, 6]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
def fusion(tab1, tab2):
    tab_fusion = []
    i1 = 0
    i2 = 0
    while i1 < len(tab1) and i2 < len(tab2):
        if tab1[i1] < tab2[i2]:
            tab_fusion.append(tab1[i1])
            i1 += 1
        else:
            tab_fusion.append(tab2[i2])
            i2 += 1

    if i1 == len(tab1):
        while i2 < len(tab2):
            tab_fusion.append(tab2[i2])
            i2 += 1
    else:
        while i1 < len(tab1):
            tab_fusion.append(tab1[i1])
            i1 += 1        

    return tab_fusion

➡ Rédigez votre code sur Basthon

Exercice 07.2

Le but de cet exercice est d’écrire une fonction récursive traduire_romain qui prend en paramètre une chaîne de caractères, non vide, représentant un nombre écrit en chiffres romains et qui renvoie son écriture décimale.

Les chiffres romains considérés sont : I, V, X, L, C, D et M. Ils représentent respectivement les nombres 1, 5, 10, 50, 100, 500, et 1000 en base dix.

On dispose d’un dictionnaire romains dont les clés sont les caractères apparaissant dans l’écriture en chiffres romains et les valeurs sont les nombres entiers associés en écriture décimale :

romains = {"I":1, "V":5, "X":10, "L":50, "C":100, "D":500, "M":1000}

Le code de la fonction traduire_romain fournie repose sur le principe suivant :

  • la valeur d’un caractère est ajoutée à la valeur du reste de la chaîne si ce caractère a une valeur supérieure (ou égale) à celle du caractère qui le suit ;

  • la valeur d’un caractère est retranchée à la valeur du reste de la chaîne si ce caractère a une valeur strictement inférieure à celle du caractère qui le suit.

Ainsi, XIV correspond au nombre 10 + 5 - 1 puisque :

  • la valeur de X (10) est supérieure à celle de I (1), on ajoute donc 10 à la valeur du reste de la chaîne, c’est-à-dire IV ;

  • la valeur de I (1) est strictement inférieure à celle de V (5), on soustrait donc 1 à la valeur du reste de la chaîne, c’est-à-dire V.

On rappelle que pour priver une chaîne de caractères de son premier caractère, on utilisera l’instruction :

nom_de_variable[1:]

Par exemple, si la variable mot contient la chaîne "CDI", mot[1:] renvoie "DI".

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
romains = {"I":1, "V":5, "X":10, "L":50, "C":100, "D":500, "M":1000}

def traduire_romain(nombre):
    """ Renvoie l’écriture décimale du nombre donné en chiffres
    romains """
    if len(nombre) == 1:
        return ...
    elif romains[nombre[0]] >= ...
        return romains[nombre[0]] + ...
    else:
        return ...

Compléter le code de la fonction traduire_romain et le tester.

Exemples :

>>> traduire_romain("XIV")
14
>>> traduire_romain("CXLII")
142
>>> traduire_romain("MMXXIII")
2023

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
romains = {"I":1, "V":5, "X":10, "L":50, "C":100, "D":500, "M":1000}

def traduire_romain(nombre):
    """ Renvoie l’écriture décimale du nombre donné en chiffres
    romains """
    if len(nombre) == 1:
        return romains[nombre]
    elif romains[nombre[0]] >= romains[nombre[1]]:
        return romains[nombre[0]] + traduire_romain(nombre[1:])
    else:
        return traduire_romain(nombre[1:]) - romains[nombre[0]]

➡ Complétez le code sur Basthon

Exercice 08.1

Sur le réseau social TipTop, on s’intéresse au nombre de « like » des abonnés. Les données sont stockées dans des dictionnaires où les clés sont les pseudos et les valeurs correspondantes sont les nombres de « like » comme ci-dessous :

{'Bob': 102, 'Ada': 201, 'Alice': 103, 'Tim': 50}

Écrire une fonction max_dico qui :

  • Prend en paramètre un dictionnaire dico non vide dont les clés sont des chaînes de caractères et les valeurs associées sont des entiers ;
  • Renvoie un tuple dont :
    • La première valeur est la clé du dictionnaire associée à la valeur maximale ;
    • La seconde valeur est la première valeur maximale présente dans le dictionnaire.

Exemples :

>>> max_dico({'Bob': 102, 'Ada': 201, 'Alice': 103, 'Tim': 50})
('Ada', 201)
>>> max_dico({'Alan': 222, 'Ada': 201, 'Eve': 220, 'Tim': 50})
('Alan', 222)

1
2
3
4
5
6
7
8
def max_dico(dico):
    cle_max = ''
    val_max = 0
    for cle in dico:
        if dico[cle] > val_max:
            val_max = dico[cle]
            cle_max = cle
    return (cle_max, val_max)

➡ Rédigez votre code sur Basthon

Exercice 08.2

Nous avons l’habitude de noter les expressions arithmétiques avec des parenthèses comme par exemple : (2 + 3) × 5.

Il existe une autre notation utilisée par certaines calculatrices, appelée notation postfixe, qui n’utilise pas de parenthèses. L’expression arithmétique précédente est alors obtenue en saisissant successivement 2, puis 3, puis l’opérateur +, puis 5, et enfin l’opérateur ×. On modélise cette saisie par le tableau [2, 3, '+', 5, '*'].

Autre exemple, la notation postfixe de 3 × 2 + 5 est modélisée par le tableau :

[3, 2, '*', 5, '+'].

D’une manière plus générale, la valeur associée à une expression arithmétique en notation postfixe est déterminée à l’aide d’une pile en parcourant l’expression arithmétique de gauche à droite de la façon suivante :

  • Si l’élément parcouru est un nombre, on le place au sommet de la pile ;
  • Si l’élément parcouru est un opérateur, on récupère les deux éléments situés au sommet de la pile et on leur applique l’opérateur. On place alors le résultat au sommet de la pile.
  • À la fin du parcours, il reste alors un seul élément dans la pile qui est le résultat de l’expression arithmétique.

Dans le cadre de cet exercice, on se limitera aux opérations × et +.

Pour cet exercice, on dispose d’une classe Pile qui implémente les méthodes de base sur la structure de pile.

Compléter le script de la fonction eval_expression qui reçoit en paramètre une liste python représentant la notation postfixe d’une expression arithmétique et qui renvoie sa valeur associée.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Pile:
    """Classe définissant une structure de pile."""
    def __init__(self):
        self.contenu = []

    def est_vide(self):
        """Renvoie le booléen True si la pile est vide, False sinon."""
        return self.contenu == []

    def empiler(self, v):
        """Place l'élément v au sommet de la pile"""
        self.contenu.append(v)

    def depiler(self):
        """
        Retire et renvoie l’élément placé au sommet de la pile,
        si la pile n’est pas vide.
        """
        if not self.est_vide():
            return self.contenu.pop()


def eval_expression(tab):
    p = Pile()
    for ... in tab:
        if element != '+' ... element != '*':
            p.empiler(...)
        else:
            if element == ...:
                resultat = p.depiler() + ...
            else:
                resultat = ...
            p.empiler(...)
    return ...

Exemple :

>>> eval_expression([2, 3, '+', 5, '*'])
25

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Pile:
    """Classe définissant une structure de pile."""
    def __init__(self):
        self.contenu = []

    def est_vide(self):
        """Renvoie le booléen True si la pile est vide, False sinon."""
        return self.contenu == []

    def empiler(self, v):
        """Place l'élément v au sommet de la pile"""
        self.contenu.append(v)

    def depiler(self):
        """
        Retire et renvoie l’élément placé au sommet de la pile,
        si la pile n’est pas vide.
        """
        if not self.est_vide():
            return self.contenu.pop()


def eval_expression(tab):
    p = Pile()
    for element in tab:
        if element != '+' and element != '*':
            p.empiler(element)
        else:
            if element == '+':
                resultat = p.depiler() + p.depiler()
            else:
                resultat = p.depiler() * p.depiler()
            p.empiler(resultat)
    return p.depiler()

➡ Complétez le code sur Basthon

Exercice 09.1

Programmer la fonction multiplication, prenant en paramètres deux nombres entiers n1 et n2, et qui renvoie le produit de ces deux nombres. Les seules opérations autorisées sont l’addition et la soustraction.

Exemples : 

>>> multiplication(3,5)
15
>>> multiplication(-4,-8)
32
>>> multiplication(-2,6)
-12
>>> multiplication(-2,0)
0


1
2
3
4
5
6
7
8
9
def multiplication(n1, n2):
    if n1 < 0:
        return -multiplication(-n1, n2)
    if n2 < 0:
        return -multiplication(n1, -n2)
    resultat = 0
    for _ in range(n2):
        resultat += n1
    return resultat

➡ Rédigez votre code sur Basthon

Exercice 09.2

Soit tab un tableau non vide d'entiers triés dans l'ordre croissant et n un entier.

La fonction chercher ci-dessous doit renvoyer un indice où la valeur n apparaît dans tab si cette valeur y figure et None sinon.

Les paramètres de la fonction sont :

  • tab, le tableau dans lequel s'effectue la recherche ;
  • n, l'entier à chercher dans le tableau ;
  • i, l'indice de début de la partie du tableau où s'effectue la recherche ;
  • j, l'indice de fin de la partie du tableau où s'effectue la recherche.

L’algorithme demandé est une recherche dichotomique récursive.

Recopier et compléter le code de la fonction chercher suivante :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def chercher(tab, n, i, j):
    if i < 0 or j > len(tab) :
        return None
    if i > j :
        return None
    m = (i + j) // ...
    if ... < n :
        return chercher(tab, n, ... , ...)
    elif ... > n :
        return chercher(tab, n, ... , ... )
    else :
        return ...

L'exécution du code doit donner : 

>>> chercher([1, 5, 6, 6, 9, 12], 7, 0, 10)

>>> chercher([1, 5, 6, 6, 9, 12], 7, 0, 5)

>>> chercher([1, 5, 6, 6, 9, 12], 9, 0, 5)
4
>>> chercher([1, 5, 6, 6, 9, 12], 6, 0, 5)
2


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def chercher(tab, n, i, j):
    if i < 0 or j > len(tab) :
        return None
    if i > j :
        return None
    m = (i + j) // 2
    if tab[m] < n :
        return chercher(tab, n, m+1 , j)
    elif tab[m] > n :
        return chercher(tab, n, i , m-1 )
    else :
        return m

➡ Complétez le code sur Basthon

Exercice 10.1

Écrire la fonction maxliste, prenant en paramètre un tableau non vide de nombres tab (de type list) et renvoyant le plus grand élément de ce tableau.

Exemples :

>>> maxliste([98, 12, 104, 23, 131, 9])
131
>>> maxliste([-27, 24, -3, 15])
24

1
2
3
4
5
6
def maxliste(tab):
    maximum = tab[0]
    for element in tab:
        if element > maximum:
            maximum = element
    return maximum

➡ Rédigez votre code sur Basthon

Exercice 10.2

On dispose de chaînes de caractères contenant uniquement des parenthèses ouvrantes et fermantes.

Un parenthésage est correct si :

  • le nombre de parenthèses ouvrantes de la chaîne est égal au nombre de parenthèses fermantes.
  • en parcourant la chaîne de gauche à droite, le nombre de parenthèses déjà ouvertes doit être, à tout moment, supérieur ou égal au nombre de parenthèses déjà fermées.

Ainsi, ((()())(())) est un parenthésage correct.

Les parenthésages ())(() et (())(() sont, eux, incorrects.

On dispose du code de la classe Pile suivant :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Pile:
    """ Classe définissant une pile """
    def __init__(self):
        self.valeurs = []

    def est_vide(self):
        """Renvoie True si la pile est vide, False sinon"""
        return self.valeurs == []

    def empiler(self, c):
        """Place l’élément c au sommet de la pile"""
        self.valeurs.append(c)

    def depiler(self):
        """Supprime l’élément placé au sommet de la pile, à condition qu’elle soit non vide"""
        if self.est_vide() == False:
            self.valeurs.pop()

On souhaite programmer une fonction parenthesage qui prend en paramètre une chaîne de caractères ch formée de parenthèses et renvoie True si la chaîne est bien parenthésée et False sinon.

Cette fonction utilise une pile et suit le principe suivant : en parcourant la chaîne de gauche à droite, si on trouve une parenthèse ouvrante, on l’empile au sommet de la pile et si on trouve une parenthèse fermante, on dépile (si possible) la parenthèse ouvrante stockée au sommet de la pile.

La chaîne est alors bien parenthésée si, à la fin du parcours, la pile est vide.

Elle est, par contre, mal parenthésée :

  • si dans le parcours, on trouve une parenthèse fermante, alors que la pile est vide ;
  • ou si, à la fin du parcours, la pile n’est pas vide.
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def parenthesage(ch):
    """Renvoie True si la chaîne ch est bien parenthésée et False sinon"""
    p = Pile()
    for c in ch:
        if c == ...:
            p.empiler(c)
        elif c == ...:
            if p.est_vide():
                return ...
            else:
                ...
    return p.est_vide()

Compléter le code de la fonction parenthesage.

Exemples :

>>> parenthesage("((()())(()))")
True
>>> parenthesage("())(()")
False
>>> parenthesage("(())(()")
False

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Pile:
    """ Classe définissant une pile """
    def __init__(self):
        self.valeurs = []

    def est_vide(self):
        """Renvoie True si la pile est vide, False sinon"""
        return self.valeurs == []

    def empiler(self, c):
        """Place l’élément c au sommet de la pile"""
        self.valeurs.append(c)

    def depiler(self):
        """Supprime l’élément placé au sommet de la pile, à condition qu’elle soit non vide"""
        if self.est_vide() == False:
            self.valeurs.pop()

def parenthesage(ch):
    """Renvoie True si la chaîne ch est bien parenthésée et False sinon"""
    p = Pile()
    for c in ch:
        if c == '(':
            p.empiler(c)
        elif c == ')':
            if p.est_vide():
                return False
            else:
                p.depiler()
    return p.est_vide()

➡ Complétez le code sur Basthon

Exercice 11.1

On modélise la représentation binaire d'un entier non signé par un tableau d'entiers dont les éléments sont 0 ou 1. Par exemple, le tableau [1, 0, 1, 0, 0, 1, 1] représente l'écriture binaire de l'entier dont l'écriture décimale est 2**6 + 2**4 + 2**1 + 2**0 = 83.

À l'aide d'un parcours séquentiel, écrire la fonction convertir répondant aux spécifications suivantes :

def convertir(tab):
    """
    tab est un tableau d'entiers, dont les éléments sont 0 ou 1 et
    représentant un entier écrit en binaire. Renvoie l'écriture
    décimale de l'entier positif dont la représentation binaire
    est donnée par le tableau tab
    """
Exemple : 
>>> convertir([1, 0, 1, 0, 0, 1, 1])
83
>>> convertir([1, 0, 0, 0, 0, 0, 1, 0])
130


1
2
3
4
5
6
7
def convertir(tab):
    puissance = 0
    total = 0
    for i in range(len(tab)-1, -1, -1):
        total += tab[i]*(2**puissance)
        puissance += 1
    return total

➡ Rédigez votre code sur Basthon

Exercice 11.2

La fonction tri_insertion suivante prend en argument une liste tab et trie cette liste en utilisant la méthode du tri par insertion. Compléter cette fonction pour qu'elle réponde à la spécification demandée.

On rappelle le principe du tri par insertion : on considère les éléments à trier un par un, le premier élément constituant, à lui tout seul, une liste triée de longueur 1. On range ensuite le second élément pour constituer une liste triée de longueur 2, puis on range le troisième élément pour avoir une liste triée de longueur 3 et ainsi de suite… A chaque étape, le premier élément de la sous-liste non triée est placé dans la sous-liste des éléments déjà triés de sorte que cette sous-liste demeure triée.

Le principe du tri par insertion est donc d'insérer à la n-ième itération, le n-ième élément à la bonne place.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def tri_insertion(tab):
    n = len(tab)
    for i in range(1, n):
        valeur_insertion = tab[...]
        # la variable j sert à déterminer où placer la valeur à ranger
        j = ...
        # tant qu'on a pas trouvé la place de l'élément à insérer
        # on décale les valeurs du tableau vers la droite
        while j > ... and valeur_insertion < tab[...]:
            tab[j] = tab[j-1]
            j = ...
        tab[j] = ...

Exemples : 

>>> liste = [9, 5, 8, 4, 0, 2, 7, 1, 10, 3, 6]
>>> tri_insertion(liste)
>>> liste
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def tri_insertion(tab):
    n = len(tab)
    for i in range(1, n):
        valeur_insertion = tab[i]
        # la variable j sert à déterminer où placer la valeur à ranger
        j = i
        # tant qu'on a pas trouvé la place de l'élément à insérer
        # on décale les valeurs du tableau vers la droite
        while j > 0 and valeur_insertion < tab[j-1]:
            tab[j] = tab[j-1]
            j = j - 1
        tab[j] = valeur_insertion

➡ Complétez le code sur Basthon

Exercice 12.1

On considère la classe ABR, dont le constructeur est le suivant :

class ABR:
    def __init__(self, g0, v0, d0):
        self.gauche = g0
        self.cle = v0
        self.droit = d0

    def __repr__(self):
        if self is None:
            return ''
        else:
            return '(' + (self.gauche).__repr__() + ',' + str(self.cle) + ',' +(self.droit).__repr__() + ')'

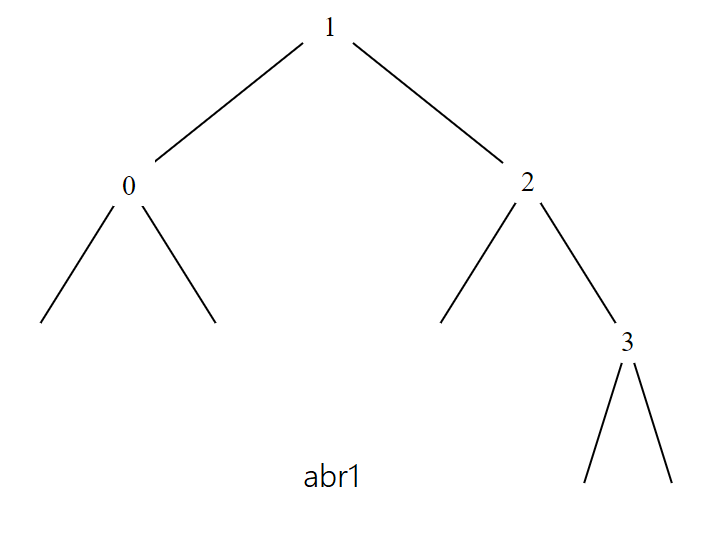
image

Ainsi, l’arbre binaire de recherche abr1 ci- contre est créé par le code python ci- dessous

n0 = ABR(None, 0, None)
n3 = ABR(None, 3, None)
n2 = ABR(None, 2, n3)
n3 = ABR(n0, 1, n2)

Dans tout le code, None correspondra à un arbre vide.

La classe ABR dispose aussi d’une méthode de représentation (__repr__ ), qui affiche entre parenthèses le contenu du sous arbre gauche, puis la clé de l’arbre, et enfin le contenu du sous arbre droit. Elle s’utilise en console de la manière suivante :

>>> abr1
((None,0,None),1,(None,2,(None,3,None)))

Écrire une fonction récursive ajoute(cle, a) qui prend en paramètres une clé cle et un arbre binaire de recherche a , et qui renvoie un arbre binaire de recherche dans lequel cle a été insérée. Dans le cas où cle est déjà présente dans a, la fonction renvoie l’arbre a inchangé.

Résultats à obtenir :

>>> a = ajoute(4, abr1)
>>> a
((None,0,None),1,(None,2,(None,3,(None,4,None))))

>>> ajoute(-5, abr1)
(((None,-5,None),0,None),1,(None,2,(None,3,None)))

>>> ajoute(2, abr1)
((None,0,None),1,(None,2,(None,3,None)))

1
2
3
4
5
6
7
8
def ajoute(cle, a): 
    if a is None:
        a = ABR(None, cle, None)
    elif cle > a.cle:
        a.droit = ajoute(cle, a.droit)
    elif cle < a.cle:
        a.gauche = ajoute(cle, a.gauche)
    return a

➡ Rédigez votre code sur Basthon

Exercice 12.2

On dispose d’un ensemble d’objets dont on connaît, pour chacun, la masse. On souhaite ranger l’ensemble de ces objets dans des boites identiques de telle manière que la somme des masses des objets contenus dans une boîte ne dépasse pas la capacité c de la boîte. On souhaite utiliser le moins de boîtes possibles pour ranger cet ensemble d’objets.

Pour résoudre ce problème, on utilisera un algorithme glouton consistant à placer chacun des objets dans la première boîte où cela est possible.

Par exemple, pour ranger dans des boîtes de capacité c = 5 un ensemble de trois objets dont les masses sont représentées en Python par la liste [1, 5, 2], on procède de la façon suivante :

  • Le premier objet, de masse 1, va dans une première boite.
  • Le deuxième objet, de masse 5, ne peut pas aller dans la même boite que le premier objet car cela dépasserait la capacité de la boite. On place donc cet objet dans une deuxième boîte.
  • Le troisième objet, de masse 2, va dans la première boîte.

On a donc utilisé deux boîtes de capacité c = 5 pour ranger les 3 objets.

Compléter la fonction Python empaqueter(liste_masses, c) suivante pour qu’elle renvoie le nombre de boîtes de capacité c nécessaires pour empaqueter un ensemble d’objets dont les masses sont contenues dans la liste liste_masses.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def empaqueter(liste_masses, c):
    n = len(liste_masses)
    nb_boites = 0
    boites = [0]*n
    for masse in ... :
        i = 0
        while i <= nb_boites and boites[i] + ... > C:
            i = i + 1
        if i == nb_boites + 1:
            ...
        boites[i] = ...
    return ...

Tester ensuite votre fonction : 

>>> empaqueter([7, 6, 3, 4, 8, 5, 9, 2], 11)
5


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def empaqueterR(liste_masses, c):
    n = len(liste_masses)
    nb_boites = 0
    boites = [0]*n
    for masse in liste_masses :
        i = 0
        while i <= nb_boites and boites[i] + masse > c:
            i = i + 1
        if i == nb_boites + 1:
            nb_boites = nb_boites + 1
        boites[i] = boites[i] + masse
    return nb_boites + 1

➡ Complétez le code sur Basthon

Exercice 13.1

Écrire en langage Python une fonction recherche prenant comme paramètres une variable a de type numérique (float ou int) et un tableau tab (type list) et qui renvoie le nombre d'occurrences de a dans tab.

Exemples : 

>>> recherche(5, [])
0
>>> recherche(5, [-2, 3, 4, 8])
0
>>> recherche(5, [-2, 3, 1, 5, 3, 7, 4])
1
>>> recherche(5, [-2, 5, 3, 5, 4, 5])
3


1
2
3
4
5
6
def recherche(a, tab):
    nb = 0
    for element in tab:
        if element == a:
            nb += 1
    return nb

➡ Rédigez votre code sur Basthon

Exercice 13.2

La fonction rendu_monnaie prend en paramètres deux nombres entiers positifs somme_due et somme_versee et elle permet de procéder au rendu de monnaie de la différence somme_versee – somme_due pour des achats effectués avec le système de pièces de la zone Euro. On utilise pour cela un algorithme glouton qui commence par rendre le maximum de pièces de plus grandes valeurs et ainsi de suite. Par la suite, on assimilera les billets à des pièces.

La fonction rendu_monnaie renvoie un tableau de type list contenant les pièces qui composent le rendu.

Toutes les sommes sont exprimées en euros. Les valeurs possibles pour les pièces sont donc [1, 2, 5, 10, 20, 50, 100, 200].

Ainsi, l’instruction rendu_monnaie(452, 500) renvoie le tableau [20, 20, 5, 2, 1].

En effet, la somme à rendre est de 48 euros soit 20 + 20 + 5 + 2 + 1.

Le code de la fonction rendu_monnaie est donné ci-dessous :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def rendu_monnaie(somme_due, somme_versee):
    pieces = [1, 2, 5, 10, 20, 50, 100, 200]
    rendu = ...
    a_rendre = ...
    i = len(pieces) - 1
    while a_rendre > ... :
        if pieces[i] <= a_rendre :
            rendu.append(...)
            a_rendre = ...
        else :
            i = ...
    return rendu

Compléter ce code et le tester : 

>>> rendu_monnaie(700,700)
[]
>>> rendu_monnaie(102,500)
[200, 100, 50, 20, 20, 5, 2, 1]


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def rendu_monnaie(somme_due, somme_versee):
    pieces = [1, 2, 5, 10, 20, 50, 100, 200]
    rendu = []
    a_rendre = somme_versee - somme_due
    i = len(pieces) - 1
    while a_rendre > 0 :
        if pieces[i] <= a_rendre :
            rendu.append(pieces[i])
            a_rendre = a_rendre - pieces[i]
        else :
            i = i - 1
    return rendu

➡ Complétez le code sur Basthon

Exercice 14.1

Écrire une fonction recherche qui prend en paramètres elt un nombre entier et tab un tableau de nombres entiers, et qui renvoie l’indice de la première occurrence de elt dans tab si elt est dans tab et -1 sinon.

Ne pas oublier d’ajouter au corps de la fonction une documentation et une ou plusieurs assertions pour vérifier les pré-conditions.

Exemples : 

>>> recherche(1, [2, 3, 4])
-1
>>> recherche(1, [10, 12, 1, 56])
2
>>> recherche(50, [1, 50, 1])
1
>>> recherche(15, [8, 9, 10, 15])
3


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
def recherche(elt, tab):
    '''
    renvoie l’indice de la première occurrence de
    elt dans tab si elt est dans tab et -1 sinon. 
    '''
    assert tab != [], "le tableau est vide"
    for i in range(len(tab)):
        if tab[i] == elt:
            return i        
    return -1

➡ Rédigez votre code sur Basthon

Exercice 14.2

On considère la fonction insere ci-dessous qui prend en argument un entier a et un tableau tab d'entiers triés par ordre croissant. Cette fonction crée et renvoie un nouveau tableau à partir de celui fourni en paramètre en y insérant la valeur a de sorte que le tableau renvoyé soit encore trié par ordre croissant. Les tableaux seront représentés sous la forme de listes Python.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
def insere(a, tab):
    """
    Insère l'élément a (int) dans le tableau tab (list)
    trié par ordre croissant à sa place et renvoie le
    nouveau tableau.
    """
    l = list(tab) #l contient les mêmes éléments que tab
    l.append(a)
    i = ...
    while a < ... and i >= 0:
        l[i+1] = ...
        l[i] = a
        i = ...
    return l

Compléter la fonction insere ci-dessus.

Exemples : 

>>> insere(3, [1, 2, 4, 5])
[1, 2, 3, 4, 5]
>>> insere(30, [1, 2, 7, 12, 14, 25])
[1, 2, 7, 12, 14, 25, 30]
>>> insere(1, [2, 3, 4])
[1, 2, 3, 4]
>>> insere(1, [])
[1]


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
def insere(a, tab):
    """
    Insère l'élément a (int) dans le tableau tab (list)
    trié par ordre croissant à sa place et renvoie le
    nouveau tableau.
    """
    l = list(tab) #l contient les mêmes éléments que tab
    l.append(a)
    i = len(l) - 2
    while a < l[i] and i >= 0:
        l[i+1] = l[i]
        l[i] = a
        i = i - 1
    return l

➡ Complétez le code sur Basthon

Exercice 15.1

On a relevé les valeurs moyennes annuelles des températures à Paris pour la période allant de 2013 à 2019. Les résultats ont été récupérés sous la forme de deux listes : l’une pour les températures, l’autre pour les années : 

t_moy = [14.9, 13.3, 13.1, 12.5, 13.0, 13.6, 13.7]
annees = [2013, 2014, 2015, 2016, 2017, 2018, 2019]

Écrire la fonction mini qui prend en paramètres un tableau releve des relevés et un tableau date des dates et qui renvoie la plus petite valeur relevée au cours de la période et l’année correspondante. On suppose que la température minimale est atteinte une seule fois.

Exemple : 

>>> mini(t_moy, annees)
(12.5, 2016)


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
t_moy = [14.9, 13.3, 13.1, 12.5, 13.0, 13.6, 13.7]
annees = [2013, 2014, 2015, 2016, 2017, 2018, 2019]

def mini(releve, date):
    temp_mini = releve[0]
    date_mini = date[0]
    for i in range(len(releve)):
        if releve[i] < temp_mini:
            temp_mini = releve[i]
            date_mini = date[i]
    return temp_mini, date_mini

➡ Rédigez votre code sur Basthon

Exercice 15.2

Un mot palindrome peut se lire de la même façon de gauche à droite ou de droite à gauche : bob, radar, et non sont des mots palindromes.

De même certains nombres sont eux aussi des palindromes : 33, 121, 345543.

L’objectif de cet exercice est d’obtenir un programme Python permettant de tester si un nombre est un nombre palindrome.

Pour remplir cette tâche, on vous demande de compléter le code des trois fonctions ci- dessous sachant que la fonction est_nbre_palindrome s’appuiera sur la fonction est_palindrome qui elle-même s’appuiera sur la fonction inverse_chaine.

La fonction inverse_chaine inverse l'ordre des caractères d'une chaîne de caractères chaine et renvoie la chaîne inversée.

La fonction est_palindrome teste si une chaine de caractères chaine est un palindrome. Elle renvoie True si c’est le cas et False sinon. Cette fonction s’appuie sur la fonction précédente.

La fonction est_nbre_palindrome teste si un nombre nbre est un palindrome. Elle renvoie True si c’est le cas et False sinon. Cette fonction s’appuie sur la fonction précédente.

Compléter le code des trois fonctions ci-dessous.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
def inverse_chaine(chaine):
    result = ...
    for caractere in chaine:
        result = ...
    return result

def est_palindrome(chaine):
    inverse = inverse_chaine(chaine)
    return ...

def est_nbre_palindrome(nbre):
    chaine = ...
    return est_palindrome(chaine)
Exemples :

>>> inverse_chaine('bac')
'cab'
>>> est_palindrome('NSI')
False
>>> est_palindrome('ISN-NSI')
True
>>> est_nbre_palindrome(214312)
False
>>> est_nbre_palindrome(213312)
True

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
def inverse_chaine(chaine):
    result = ''
    for caractere in chaine:
        result = caractere + result
    return result

def est_palindrome(chaine):
    inverse = inverse_chaine(chaine)
    return chaine == inverse

def est_nbre_palindrome(nbre):
    chaine = str(nbre)
    return est_palindrome(chaine)

➡ Complétez le code sur Basthon

Exercice 16.1

Écrire une fonction recherche_indices_classement qui prend en paramètres un entier elt et une liste d’entiers tab, et qui renvoie trois listes :

  • la première liste contient les indices des valeurs de la liste tab strictement inférieures à elt ;
  • la deuxième liste contient les indices des valeurs de la liste tab égales à elt ;
  • la troisième liste contient les indices des valeurs de la liste tab strictement supérieures à elt.

Exemples :

>>> recherche_indices_classement(3, [1, 3, 4, 2, 4, 6, 3, 0])
([0, 3, 7], [1, 6], [2, 4, 5])
>>> recherche_indices_classement(3, [1, 4, 2, 4, 6, 0])
([0, 2, 5], [], [1, 3, 4])
>>>recherche_indices_classement(3, [1, 1, 1, 1])
([0, 1, 2, 3], [], [])
>>> recherche_indices_classement(3, [])
([], [], [])

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def recherche_indices_classement(elt, tab):
    ind_inf = []
    ind_egal = []
    ind_sup = [] 
    for i in range(len(tab)):
        if tab[i] < elt:
            ind_inf.append(i)
        elif tab[i] > elt:
            ind_sup.append(i)
        else:
            ind_egal.append(i)
    return (ind_inf, ind_egal, ind_sup)

➡ Rédigez votre code sur Basthon

Exercice 16.2

Un professeur de NSI décide de gérer les résultats de sa classe sous la forme d’un dictionnaire :

  • les clefs sont les noms des élèves ;
  • les valeurs sont des dictionnaires dont les clefs sont les types d’épreuves sous forme de chaîne de caractères et les valeurs sont les notes obtenues associées à leurs coefficients dans une liste.

Avec :

resultats = {'Dupont': {
                        'DS1': [15.5, 4],
                        'DM1': [14.5, 1],
                        'DS2': [13, 4],
                        'PROJET1': [16, 3],
                        'DS3': [14, 4]
                    },
            'Durand': {
                        'DS1': [6 , 4],
                        'DM1': [14.5, 1],
                        'DS2': [8, 4],
                        'PROJET1': [9, 3],
                        'IE1': [7, 2],
                        'DS3': [8, 4],
                        'DS4':[15, 4]
                    }
            }

L’élève dont le nom est Durand a ainsi obtenu au DS2 la note de 8 avec un coefficient 4.

Le professeur crée une fonction moyenne qui prend en paramètre le nom d’un de ses élèves et renvoie sa moyenne arrondie au dixième.

Compléter le code du professeur ci-dessous :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def moyenne(nom, dico_result):
    if nom in ...:
        notes = dico_result[nom]
        total_points = ...
        total_coefficients = ...
        for ...  in notes.values():
            note, coefficient = valeurs
            total_points = total_points + ... * coefficient
            total_coefficients = ... + coefficient
        return round( ... / total_coefficients, 1 )
    else:
        return -1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def moyenne(nom, dico_result):
    if nom in dico_result:
        notes = dico_result[nom]
        total_points = 0.
        total_coefficients = 0
        for valeurs  in notes.values():
            note, coefficient = valeurs
            total_points = total_points + note * coefficient
            total_coefficients = total_coefficients + coefficient
        return round( total_points / total_coefficients, 1 )
    else:
        return -1

➡ Complétez le code sur Basthon

Exercice 17.1

Écrire une fonction moyenne(liste_notes) qui renvoie la moyenne pondérée des résultats contenus dans la liste liste_notes, non vide, donnée en paramètre. Cette liste contient des couples (note, coefficient) dans lesquels :

  • note est un nombre de type flottant (float) compris entre 0 et 20 ;
  • coefficient est un nombre entier strictement positif.

Ainsi l’expression moyenne([(15,2),(9,1),(12,3)]) devra renvoyer 12.5.

\(\dfrac{2 \times 15 + 1 \times 9 + 3 \times 12 }{2+1+3}=12,5\)

1
2
3
4
5
6
7
8
9
def moyenne(liste_notes):
    somme_notes = 0
    somme_coeffs = 0
    for devoir in liste_notes:
        note = devoir[0]
        coeff = devoir[1]
        somme_notes += note * coeff
        somme_coeffs += coeff
    return somme_notes / somme_coeffs

➡ Rédigez votre code sur Basthon

Exercice 17.2

On cherche à déterminer les valeurs du triangle de Pascal (Figure 1).

Dans le triangle de Pascal, chaque ligne commence et se termine par le nombre 1. Comme l’illustre la Figure 2, on additionne deux valeurs successives d’une ligne pour obtenir la valeur qui se situe sous la deuxième valeur.

image

Compléter la fonction pascal ci-après prenant en paramètre un entier n supérieur ou égal à 2. Cette fonction doit renvoyer une liste correspondant au triangle de Pascal de la ligne 0 à la ligne n. Le tableau représentant le triangle de Pascal sera contenu dans la variable triangle.

1
2
3
4
5
6
7
8
9
def pascal(n):
    triangle = [[1]]
    for k in range(1,...):
        ligne_k = [...]
        for i in range(1,k):
            ligne_k.append(triangle[...][i-1]+triangle[...][...])
        ligne_k.append(...)
        triangle.append(ligne_k)
    return triangle

Pour n = 4, voici ce qu'on devra obtenir : 

>>> pascal(4)
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1]]
Pour n = 5, voici ce qu'on devra obtenir : 
>>> pascal(5)
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1], [1, 5, 10, 10, 5, 1]]


1
2
3
4
5
6
7
8
9
def pascal(n):
    triangle = [[1]]
    for k in range(1, n+1):
        ligne_k = [1]
        for i in range(1, k):
            ligne_k.append(triangle[k-1][i-1] + triangle[k-1][i])
        ligne_k.append(1)
        triangle.append(ligne_k)
    return triangle

➡ Complétez le code sur Basthon

Exercice 18.1

Écrire une fonction max_et_indice qui prend en paramètre une liste non vide tab de nombres entiers et qui renvoie la valeur du plus grand élément de cette liste ainsi que l’indice de sa première apparition dans cette liste.

L’utilisation de la fonction native max n’est pas autorisée.

Ne pas oublier d’ajouter au corps de la fonction une documentation et une ou plusieurs assertions pour vérifier les pré-conditions.

Exemples :

>>> max_et_indice([1, 5, 6, 9, 1, 2, 3, 7, 9, 8])
(9, 3)
>>> max_et_indice([-2])
(-2, 0)
>>> max_et_indice([-1, -1, 3, 3, 3])
(3, 2)
>>> max_et_indice([1, 1, 1, 1])
(1, 0)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
def max_et_indice(tab):
    '''
    renvoie la valeur du plus grand élément de cette liste ainsi
    que l’indice de sa première apparition dans cette liste.
    '''
    assert tab != [], 'le tableau est vide'

    val_max = tab[0]
    ind_max = 0
    for i in range(len(tab)):
        if tab[i] > val_max:
            val_max = tab[i]
            ind_max = i
    return (val_max, ind_max)

➡ Rédigez votre code sur Basthon

Exercice 18.2

L’ordre des gènes sur un chromosome est représenté par un tableau ordre de n cases d’entiers distincts deux à deux et compris entre 1 et n.

Par exemple, ordre = [5, 4, 3, 6, 7, 2, 1, 8, 9] dans le cas n = 9.

On dit qu’il y a un point de rupture dans ordre dans chacune des situations suivantes :

  • la première valeur de ordre n’est pas 1 ;
  • l’écart entre deux gènes consécutifs n’est pas égal à 1 ;
  • la dernière valeur de ordre n’est pas n.

Par exemple, si ordre = [5, 4, 3, 6, 7, 2, 1, 8, 9] avec n = 9, on a

  • un point de rupture au début car 5 est différent de 1
  • un point de rupture entre 3 et 6 (l’écart est de 3)
  • un point de rupture entre 7 et 2 (l’écart est de 5)
  • un point de rupture entre 1 et 8 (l’écart est de 7)

Il y a donc 4 points de rupture.

Compléter les fonctions Python est_un_ordre et nombre_points_rupture proposées à la page suivante pour que :

  • la fonction est_un_ordre renvoie True si le tableau passé en paramètre représente bien un ordre de gènes de chromosome et False sinon ;

  • la fonction nombre_points_rupture renvoie le nombre de points de rupture d’un tableau passé en paramètre représentant l’ordre de gènes d’un chromosome.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def est_un_ordre(tab):
    '''
    Renvoie True si tab est de longueur n et contient tous les entiers
    de 1 à n, False sinon
    '''
    for i in range(1,...):
        if ...:
            return False
    return True


def nombre_points_rupture(ordre):
    '''
    Renvoie le nombre de point de rupture de ordre qui représente un ordre
    de gènes de chromosome
    '''
    assert ... # ordre n'est pas un ordre de gènes
    n = len(ordre)
    nb = 0
    if ordre[...] != 1: # le premier n'est pas 1
        nb = nb + 1
    i = 0
    while i < ...:
        if ... not in [-1, 1]: # l'écart n'est pas 1
            nb = nb + 1
        i = i + 1
    if ordre[...] != n: # le dernier n'est pas n
        nb = nb + 1
    return nb

Exemples :

>>> est_un_ordre([1, 6, 2, 8, 3, 7])
False
>>> est_un_ordre([5, 4, 3, 6, 7, 2, 1, 8, 9])
True
>>> nombre_points_rupture([5, 4, 3, 6, 7, 2, 1, 8, 9])
4
>>> nombre_points_rupture([1, 2, 3, 4, 5])
0
>>> nombre_points_rupture([1, 6, 2, 8, 3, 7, 4, 5])
7
>>> nombre_points_rupture([2, 1, 3, 4])
2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def est_un_ordre(tab):
    '''
    Renvoie True si tab est de longueur n et contient tous les entiers
    de 1 à n, False sinon
    '''
    for i in range(1, len(tab)+1):
        if i not in tab:
            return False
    return True


def nombre_points_rupture(ordre):
    '''
    Renvoie le nombre de point de rupture de ordre qui représente un ordre
    de gènes de chromosome
    '''
    assert est_un_ordre(ordre) # ordre n'est pas un ordre de gènes
    n = len(ordre)
    nb = 0
    if ordre[0] != 1: # le premier n'est pas 1
        nb = nb + 1
    i = 0
    while i < n-1:
        if ordre[i+1] - ordre[i] not in [-1, 1]: # l'écart n'est pas 1
            nb = nb + 1
        i = i + 1
    if ordre[n-1] != n: # le dernier n'est pas n
        nb = nb + 1
    return nb

➡ Complétez le code sur Basthon

Exercice 19.1

Écrire une fonction recherche qui prend en paramètres un tableau tab de nombres entiers triés par ordre croissant et un nombre entier n, et qui effectue une recherche dichotomique du nombre entier n dans le tableau non vide tab.

Cette fonction doit renvoyer un indice correspondant au nombre cherché s’il est dans le tableau, -1 sinon.

Exemples : 

>>> recherche([2, 3, 4, 5, 6], 5)
3
>>> recherche([2, 3, 4, 6, 7], 5)
-1


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def recherche(tab, n):
    ind_debut = 0
    ind_fin = len(tab) - 1
    while ind_debut <= ind_fin:
        ind_milieu = (ind_debut + ind_fin) // 2
        if tab[ind_milieu] == n:
            return ind_milieu
        elif tab[ind_milieu] < n:
            ind_debut = ind_milieu + 1
        else:
            ind_fin = ind_milieu - 1
    return -1

➡ Rédigez votre code sur Basthon

Exercice 19.2

Le codage de César transforme un message en changeant chaque lettre en la décalant dans l’alphabet. Par exemple, avec un décalage de 3, le A se transforme en D, le B en E, ..., le X en A, le Y en B et le Z en C. Les autres caractères (‘!’,’ ?’ ...) ne sont pas codés.

La fonction position_alphabet ci-dessous prend en paramètre un caractère lettre et renvoie la position de lettre dans la chaîne de caractères ALPHABET s’il s’y trouve.

La fonction cesar prend en paramètre une chaîne de caractères message et un nombre entier decalage et renvoie le nouveau message codé avec le codage de César utilisant le décalage decalage.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
ALPHABET = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'

def position_alphabet(lettre):
    return ord(lettre) - ord('A')

def cesar(message, decalage):
    resultat = ''
    for ... in message:
        if 'A' <= c and c <= 'Z':
            indice = ( ... ) % 26
            resultat = resultat + ALPHABET[indice]
        else:
            resultat = ...
    return resultat

Compléter la fonction cesar.

Exemples :

>>> cesar('BONJOUR A TOUS. VIVE LA MATIERE NSI !', 4)
'FSRNSYV E XSYW. ZMZI PE QEXMIVI RWM !'
>>> cesar('GTSOTZW F YTZX. ANAJ QF RFYNJWJ SXN !', -5)
'BONJOUR A TOUS. VIVE LA MATIERE NSI !'

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
ALPHABET = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'

def position_alphabet(lettre):
    return ord(lettre) - ord('A')

def cesar(message, decalage):
    resultat = ''
    for c in message:
        if 'A' <= c and c <= 'Z':
            indice = (position_alphabet(c) + decalage) % 26
            resultat = resultat + ALPHABET[indice]
        else:
            resultat = resultat + c
    return resultat

➡ Complétez le code sur Basthon

Exercice 20.1

Écrire une fonction ajoute_dictionnaires qui prend en paramètres deux dictionnaires d1 et d2 dont les clés sont des nombres et renvoie le dictionnaire d défini de la façon suivante :

  • Les clés de d sont celles de d1 et celles de d2 réunies.
  • Si une clé est présente dans les deux dictionnaires d1 et d2, sa valeur associée dans le dictionnaire d est la somme de ses valeurs dans les dictionnaires d1 et d2.
  • Si une clé n’est présente que dans un des deux dictionnaires, sa valeur associée dans le dictionnaire d est la même que sa valeur dans le dictionnaire où elle est présente.

Exemples :

>>> ajoute_dictionnaires({1: 5, 2: 7}, {2: 9, 3: 11})
{1: 5, 2: 16, 3: 11}
>>> ajoute_dictionnaires({}, {2: 9, 3: 11})
{2: 9, 3: 11}
>>> ajoute_dictionnaires({1: 5, 2: 7}, {})
{1: 5, 2: 7}

1
2
3
4
5
6
7
def ajoute_dictionnaires(d1, d2):
for cle in d2:
    if cle in d1:
        d1[cle] += d2[cle]
    else:
        d1[cle] = d2[cle]
return d1

➡ Rédigez votre code sur Basthon

Exercice 20.2

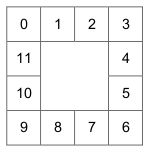
On considère une piste carrée qui contient 4 cases par côté. Les cases sont numérotées de 0 inclus à 12 exclu comme ci-dessous :

image

L’objectif de l’exercice est d’implémenter le jeu suivant :

Au départ, le joueur place son pion sur la case 0. A chaque coup, il lance un dé équilibré à six faces et avance son pion d’autant de cases que le nombre indiqué par le dé (entre 1 et 6 inclus) dans le sens des aiguilles d’une montre.

Par exemple, s’il obtient 2 au premier lancer, il pose son pion sur la case 2 puis s’il obtient 6 au deuxième lancer, il le pose sur la case 8, puis s’il obtient à nouveau 6, il pose le pion sur la case 2.

Le jeu se termine lorsque le joueur a posé son pion sur toutes les cases de la piste.

Compléter la fonction nbre_coups ci-dessous de sorte qu’elle renvoie le nombre de lancers aléatoires nécessaires pour terminer le jeu.

Proposer ensuite quelques tests pour en vérifier le fonctionnement.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
from random import randint

def nbre_coups():
    n = ...
    cases_vues = [0]
    case_en_cours = 0
    nbre_cases = 12
    while ... < ...:
        x = randint(1, 6)
        case_en_cours = (case_en_cours + ...) % ...
        if ...:
            cases_vues.append(case_en_cours)
        n = ...
    return n

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
from random import randint

def nbre_coups():
    n = 0
    cases_vues = [0]
    case_en_cours = 0
    nbre_cases = 12
    while len(cases_vues) < nbre_cases:
        x = randint(1, 6)
        case_en_cours = (case_en_cours + x) % nbre_cases
        if case_en_cours not in cases_vues:
            cases_vues.append(case_en_cours)
        n = n + 1
    return n

➡ Complétez le code sur Basthon

Exercice 21.1

Le codage par différence (delta encoding en anglais) permet de compresser un tableau de données en indiquant pour chaque donnée, sa différence avec la précédente (plutôt que la donnée elle-même). On se retrouve alors avec un tableau de données plus petit, nécessitant moins de place en mémoire. Cette méthode se révèle efficace lorsque les valeurs consécutives sont proches.

Programmer la fonction delta(liste) qui prend en paramètre un tableau non vide de nombres entiers et qui renvoie un tableau contenant les valeurs entières compressées à l’aide cette technique.

Exemples :

>>> delta([1000, 800, 802, 1000, 1003])
[1000, -200, 2, 198, 3]
>>> delta([42])
[42] 

1
2
3
4
5
def delta(tab):
    diff = [tab[0]]
    for i in range(1, len(tab)):
        diff.append(tab[i] - tab[i-1])
    return diff

➡ Rédigez votre code sur Basthon

Exercice 21.2

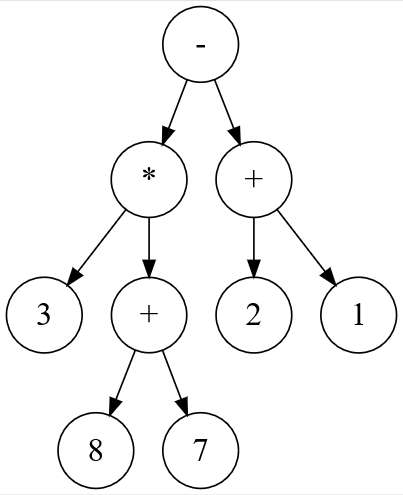
Une expression arithmétique ne comportant que les quatre opérations +, −, ×, ÷ peut être représentée sous forme d’arbre binaire. Les nœuds internes sont des opérateurs et les feuilles sont des nombres. Dans un tel arbre, la disposition des nœuds joue le rôle des parenthèses que nous connaissons bien.

image

En parcourant en profondeur infixe l’arbre binaire ci-dessus, on retrouve l’expression notée habituellement :

\[(3 \times (8 + 7)) − (2 + 1)\]

La classe Noeud ci-après permet d’implémenter une structure d’arbre binaire.

Compléter la fonction récursive expression_infixe qui prend en paramètre un objet de la classe Noeud et qui renvoie l’expression arithmétique représentée par l’arbre binaire passé en paramètre, sous forme d’une chaîne de caractères contenant des parenthèses.

Résultat attendu avec l’arbre ci-dessus :

>>> e = Noeud(Noeud(Noeud(None, 3, None), '*', Noeud(Noeud(None, 8, None),
'+', Noeud(None, 7, None))), '-', Noeud(Noeud(None, 2, None), '+',
Noeud(None, 1, None)))

>>> expression_infixe(e)
'((3*(8+7))-(2+1))'

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Noeud:
    '''
    classe implémentant un noeud d'arbre binaire
    '''

    def __init__(self, g, v, d):
        '''
        un objet Noeud possède 3 attributs :
        - gauche : le sous-arbre gauche,
        - valeur : la valeur de l'étiquette,
        - droit : le sous-arbre droit.
        '''
        self.gauche = g
        self.valeur = v
        self.droit = d

    def __str__(self):
        '''
        renvoie la représentation du noeud en chaine de caractères
        '''
        return str(self.valeur)

    def est_une_feuille(self):
        '''
        renvoie True si et seulement si le noeud est une feuille
        '''
        return self.gauche is None and self.droit is None


def expression_infixe(e):
    s = ...
    if e.gauche is not None:
        s = '(' + s + expression_infixe(...)
    s = s + ...
    if ... is not None:
        s = s + ... + ...
    return s

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Noeud:
    '''
    classe implémentant un noeud d'arbre binaire
    '''

    def __init__(self, g, v, d):
        '''
        un objet Noeud possède 3 attributs :
        - gauche : le sous-arbre gauche,
        - valeur : la valeur de l'étiquette,
        - droit : le sous-arbre droit.
        '''
        self.gauche = g
        self.valeur = v
        self.droit = d

    def __str__(self):
        '''
        renvoie la représentation du noeud en chaine de caractères
        '''
        return str(self.valeur)

    def est_une_feuille(self):
        '''
        renvoie True si et seulement si le noeud est une feuille
        '''
        return self.gauche is None and self.droit is None


def expression_infixe(e):
    s = ''
    if e.gauche is not None:
        s = '(' + s + expression_infixe(e.gauche)
    s = s + str(e.valeur)
    if e.droit is not None:
        s = s + expression_infixe(e.droit) + ')'
    return s

➡ Complétez le code sur Basthon

Exercice 22.1

On rappelle que :

  • le nombre \(a^n\) est le nombre \(a \times a \times a \times \dots \times a\), où le facteur \(a\) apparaît \(n\) fois,
  • en langage Python, l’instruction t[-1] permet d’accéder au dernier élément du tableau t.

Dans cet exercice, l’opérateur ** et la fonction pow ne sont pas autorisés.

Programmer en langage Python une fonction liste_puissances qui prend en argument un nombre entier a, un entier strictement positif n et qui renvoie la liste de ses puissances \(\rm{[a^1, a^2, ..., a^n]}\).

Programmer également une fonction liste_puisssances_borne qui prend en argument un nombre entier a supérieur ou égal à 2 et un entier borne, et qui renvoie la liste de ses puissances, à l’exclusion de \(\rm{a^0}\), strictement inférieures à borne.

Exemples :

>>> liste_puissances(3, 5)
[3, 9, 27, 81, 243]
>>> liste_puissances(-2, 4)
[-2, 4, -8, 16]
>>> liste_puissances_borne(2, 16)
[2, 4, 8]
>>> liste_puissances_borne(2, 17)
[2, 4, 8, 16]
>>> liste_puissances_borne(5, 5)
[]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
def liste_puissances(a,n):
    puissances = [a]
    for i in range(n-1):
        puissances.append(puissances[-1] * a)
    return puissances

def liste_puissances_borne(a, borne):
    lst = []
    val = a
    while val < borne:
        lst.append(val)
        val = val * a
    return lst

➡ Rédigez votre code sur Basthon

Exercice 22.2

On affecte à chaque lettre de l'alphabet un code selon le tableau ci-dessous :

A B C D E F G H I J K L M
1 2 3 4 5 6 7 8 9 10 11 12 13
N O P Q R S T U V W X Y Z
14 15 16 17 18 19 20 21 22 23 24 25 26

Pour un mot donné, on détermine d’une part son code alphabétique concaténé, obtenu par la juxtaposition des codes de chacun de ses caractères, et d’autre part, son code additionné, qui est la somme des codes de chacun de ses caractères.

Par ailleurs, on dit que ce mot est « parfait » si le code additionné divise le code concaténé.

Exemples :

  • Pour le mot "PAUL", le code concaténé est la chaîne '1612112', soit l’entier 1 612 112. Son code additionné est l’entier 50 car 16 + 1 + 21 + 12 = 50. 50 ne divise pas l’entier 1 612 112 ; par conséquent, le mot "PAUL" n’est pas parfait.

  • Pour le mot "ALAIN", le code concaténé est la chaîne '1121914', soit l’entier 1 121 914. Le code additionné est l’entier 37 car 1 + 12 + 1 + 9 + 14 = 37. 37 divise l’entier 1 121 914 ; par conséquent, le mot "ALAIN" est parfait.

Compléter la fonction est_parfait ci-dessous qui prend comme argument une chaîne de caractères mot (en lettres majuscules) et qui renvoie le code alphabétique concaténé, le code additionné de mot, ainsi qu’un booléen qui indique si mot est parfait ou pas.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
dico = {"A": 1, "B": 2, "C": 3, "D": 4, "E": 5, "F": 6,
        "G": 7, "H": 8, "I": 9, "J": 10, "K": 11, "L": 12,
        "M": 13, "N": 14, "O": 15, "P": 16, "Q": 17,
        "R": 18, "S": 19, "T": 20, "U": 21, "V": 22,
        "W": 23, "X": 24, "Y": 25, "Z": 26}


def est_parfait(mot):
    # mot est une chaîne de caractères (en lettres majuscules)
    code_concatene = ""
    code_additionne = ...
    for c in mot:
        code_concatene = code_concatene + ...
        code_additionne = ...
    code_concatene = int(code_concatene)
    if ... :
        mot_est_parfait = True
    else:
        mot_est_parfait = False
    return code_additionne, code_concatene, mot_est_parfait

Exemples : 

>>> est_parfait("PAUL")
(50, 1612112, False)
>>> est_parfait("ALAIN")
(37, 1121914, True)


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
dico = {"A": 1, "B": 2, "C": 3, "D": 4, "E": 5, "F": 6,
        "G": 7, "H": 8, "I": 9, "J": 10, "K": 11, "L": 12,
        "M": 13, "N": 14, "O": 15, "P": 16, "Q": 17,
        "R": 18, "S": 19, "T": 20, "U": 21, "V": 22,
        "W": 23, "X": 24, "Y": 25, "Z": 26}


def est_parfait(mot):
    # mot est une chaîne de caractères (en lettres majuscules)
    code_concatene = ""
    code_additionne = 0
    for c in mot:
        code_concatene = code_concatene + str(dico[c])
        code_additionne = code_additionne + dico[c]
    code_concatene = int(code_concatene)
    if code_concatene % code_additionne == 0:
        mot_est_parfait = True
    else:
        mot_est_parfait = False
    return code_additionne, code_concatene, mot_est_parfait

➡ Complétez le code sur Basthon

Exercice 23.1

On considère des tables (des tableaux de dictionnaires) qui contiennent des enregistrements relatifs à des animaux hébergés dans un refuge. Les attributs des enregistrements sont 'nom', 'espece', 'age', 'enclos'. Voici un exemple d'une telle table :

animaux = [ {'nom':'Medor', 'espece':'chien', 'age':5, 'enclos':2},
            {'nom':'Titine', 'espece':'chat', 'age':2, 'enclos':5},
            {'nom':'Tom', 'espece':'chat', 'age':7, 'enclos':4},
            {'nom':'Belle', 'espece':'chien', 'age':6, 'enclos':3},
            {'nom':'Mirza', 'espece':'chat', 'age':6, 'enclos':5}]

Programmer une fonction selection_enclos qui :

  • prend en paramètres :
    • une table table_animaux contenant des enregistrements relatifs à des animaux (comme dans l'exemple ci-dessus),
    • un numéro d'enclos num_enclos ;
  • renvoie une table contenant les enregistrements de table_animaux dont l'attribut 'enclos' est num_enclos.

Exemples avec la table animaux ci-dessus :

>>> selection_enclos(animaux, 5)
[{'nom':'Titine', 'espece':'chat', 'age':2, 'enclos':5},
 {'nom':'Mirza', 'espece':'chat', 'age':6, 'enclos':5}]

>>> selection_enclos(animaux, 2)
[{'nom':'Medor', 'espece':'chien', 'age':5, 'enclos':2}]

>>> selection_enclos(animaux, 7)
[]

1
2
3
4
5
6
def selection_enclos(table_animaux, num_enclos):
    table = []
    for animal in table_animaux:
        if animal['enclos'] == num_enclos:
            table.append(animal)
    return table

➡ Rédigez votre code sur Basthon

Exercice 23.2

On considère des tableaux de nombres dont tous les éléments sont présents exactement trois fois et à suivre, sauf un élément qui est présent une unique fois et que l'on appelle « l'intrus ». Voici quelques exemples :

tab_a = [3, 3, 3, 9, 9, 9, 1, 1, 1, 7, 2, 2, 2, 4, 4, 4, 8, 8, 8, 5, 5, 5]
#l'intrus est 7

tab_b = [8, 5, 5, 5, 9, 9, 9, 18, 18, 18, 3, 3, 3]
#l'intrus est 8

tab_c = [5, 5, 5, 1, 1, 1, 0, 0, 0, 6, 6, 6, 3, 8, 8, 8]
#l'intrus est 3
On remarque qu'avec de tels tableaux :

  • pour les indices multiples de 3 situés strictement avant l'intrus, l'élément correspondant et son voisin de droite sont égaux,
  • pour les indices multiples de 3 situés après l'intrus, l'élément correspondant et son voisin de droite - s'il existe - sont différents.

Ce que l'on peut observer ci-dessous en observant les valeurs des paires de voisins marquées par des caractères ^ :

[3, 3, 3, 9, 9, 9, 1, 1, 1, 7, 2, 2, 2, 4, 4, 4, 8, 8, 8, 5, 5, 5]
 ^  ^     ^  ^     ^  ^     ^  ^     ^  ^     ^  ^     ^  ^     ^
 0        3        6        9        12       15       18       21

Dans des listes comme celles ci-dessus, un algorithme récursif pour trouver l'intrus consiste alors à choisir un indice i multiple de 3 situé approximativement au milieu des indices parmi lesquels se trouve l'intrus.

Puis, en fonction des valeurs de l'élément d'indice i et de son voisin de droite, à appliquer récursivement l'algorithme à la moitié droite ou à la moitié gauche des indices parmi lesquels se trouve l'intrus.

Par exemple, si on s’intéresse à l’indice 12, on voit les valeurs 2 et 4 qui sont différentes : l’intrus est donc à gauche de l’indice 12 (indice 12 compris)

En revanche, si on s’intéresse à l’indice 3, on voit les valeurs 9 et 9 qui sont identiques : l’intrus est donc à droite des indices 3-4-5, donc à partir de l’indice 6.

Compléter la fonction récursive trouver_intrus proposée page suivante qui met en œuvre cet algorithme.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
def trouver_intrus(tab, g, d):
    '''
    Renvoie la valeur de l'intrus situé entre les indices g et d 
    dans la liste tab où :
    tab vérifie les conditions de l'exercice,
    g et d sont des multiples de 3.
    '''
    if g == d:
        return ...

    else:
        nombre_de_triplets = (d - g) // ...
        indice = g + 3 * (nombre_de_triplets // 2)
        if ... :
            return ...
        else:
            return ...

Exemples :

>>> trouver_intrus([3, 3, 3, 9, 9, 9, 1, 1, 1, 7, 2, 2, 2, 4, 4, 4, 8, 8,
8, 5, 5, 5], 0, 21)
7

>>> trouver_intrus([8, 5, 5, 5, 9, 9, 9, 18, 18, 18, 3, 3, 3], 0, 12)
8

>>> trouver_intrus([5, 5, 5, 1, 1, 1, 0, 0, 0, 6, 6, 6, 3, 8, 8, 8], 0, 15)
3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
def trouver_intrus(tab, g, d):
    '''
    Renvoie la valeur de l'intrus situé entre les indices g et d 
    dans la liste tab où :
    tab vérifie les conditions de l'exercice,
    g et d sont des multiples de 3.
    '''
    if g == d:
        return tab[g]

    else:
        nombre_de_triplets = (d - g) // 3
        indice = g + 3 * (nombre_de_triplets // 2)
        if tab[indice] != tab[indice + 1] :
            return trouver_intrus(tab, g, indice)
        else:
            return trouver_intrus(tab, indice + 3, d)

➡ Complétez le code sur Basthon

Exercice 24.1

Le nombre d’occurrences d’un caractère dans une chaîne de caractère est le nombre d’apparitions de ce caractère dans la chaîne.

Exemples :

  • le nombre d’occurrences du caractère ‘o’ dans ‘bonjour’ est 2 ;
  • le nombre d’occurrences du caractère ‘b’ dans ‘Bébé’ est 1 ;
  • le nombre d’occurrences du caractère ‘B’ dans ‘Bébé’ est 1 ;
  • le nombre d’occurrences du caractère ‘ ‘ dans ‘Hello world !’ est 2.

On cherche les occurrences des caractères dans une phrase. On souhaite stocker ces occurrences dans un dictionnaire dont les clefs seraient les caractères de la phrase et les valeurs l’occurrence de ces caractères.

Par exemple : avec la phrase 'Hello world !' le dictionnaire est le suivant :

{'H': 1,'e': 1,'l': 3,'o': 2,' ': 2,'w': 1,'r': 1,'d': 1,'!': 1}

L’ordre des clefs n’a pas d’importance.

Écrire une fonction nbr_occurrences prenant comme paramètre une chaîne de caractères chaine et renvoyant le dictionnaire des nombres d’occurrences des caractères de cette chaîne.

1
2
3
4
5
6
7
8
def nbr_occurrences(chaine):
    nb_occ = {}
    for caractere in chaine:
        if caractere in nb_occ:
            nb_occ[caractere] += 1
        else:
            nb_occ[caractere] = 1
    return nb_occ

➡ Rédigez votre code sur Basthon

Exercice 24.2

La fonction fusion prend deux listes lst1, lst2 d’entiers triées par ordre croissant et les fusionne en une liste triée lst12 qu’elle renvoie.

Le code Python de la fonction fusion est

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def fusion(lst1,lst2):
    n1 = len(lst1)
    n2 = len(lst2)
    lst12 = [0] * (n1 + n2)
    i1 = 0
    i2 = 0
    i = 0
    while i1 < n1 and ... :
        if lst1[i1] < lst2[i2]:
            lst12[i] = ...
            i1 = ...
        else:
            lst12[i] = lst2[i2]
            i2 = ...
        i += 1
    while i1 < n1:
        lst12[i] = ...
        i1 = i1 + 1
        i = ...
    while i2 < n2:
        lst12[i] = ...
        i2 = i2 + 1
        i = ...
    return lst12

Compléter le code.

Exemple :

>>> fusion([1, 6, 10],[0, 7, 8, 9])
[0, 1, 6, 7, 8, 9, 10]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def fusion(lst1, lst2):
    n1 = len(lst1)
    n2 = len(lst2)
    lst12 = [0] * (n1 + n2)
    i1 = 0
    i2 = 0
    i = 0
    while i1 < n1 and i2 < n2 :
        if lst1[i1] < lst2[i2]:
            lst12[i] = lst1[i1]
            i1 = i1 + 1
        else:
            lst12[i] = lst2[i2]
            i2 = i2 + 1
        i += 1
    while i1 < n1:
        lst12[i] = lst1[i1]
        i1 = i1 + 1
        i = i + 1
    while i2 < n2:
        lst12[i] = lst2[i2]
        i2 = i2 + 1
        i = i + 1
    return lst12

➡ Complétez le code sur Basthon

Exercice 25.1

Écrire une fonction enumere qui prend en paramètre une liste L et renvoie un dictionnaire d dont les clés sont les éléments de L avec pour valeur associée la liste des indices de l’élément dans la liste L.

Exemple :

>>> enumere([1, 1, 2, 3, 2, 1])
{1: [0, 1, 5], 2: [2, 4], 3: [3]}

1
2
3
4
5
6
7
8
def enumere(L):
    d = {}
    for i in range(len(L)):
        if L[i] in d:
            d[L[i]].append(i)
        else:
            d[L[i]] = [i]
    return d

➡ Rédigez votre code sur Basthon

Exercice 25.2

Un arbre binaire est implémenté par la classe Arbre donnée ci-dessous.
Les attributs fg et fd prennent pour valeurs des instances de la classe Arbre ou None.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Arbre:
    def __init__(self, etiquette):
        self.v = etiquette
        self.fg = None
        self.fd = None

def parcours(arbre, liste):
    if arbre != None:
        parcours(arbre.fg, liste)
        liste.append(arbre.v)
        parcours(arbre.fd, liste)
    return liste

La fonction récursive parcours renvoie la liste des étiquettes des nœuds de l’arbre implémenté par l’instance arbre dans l’ordre du parcours en profondeur infixe à partir d’une liste vide passée en argument.

Compléter le code de la fonction insere qui insère un nœud d’étiquette cle en feuille de l’arbre implémenté par l’instance arbre selon la spécification indiquée et de façon que l’arbre ainsi complété soit encore un arbre binaire de recherche.

Tester ensuite ce code en utilisant la fonction parcours et en insérant successivement des nœuds d’étiquette 1, 4, 6 et 8 dans l’arbre binaire de recherche représenté ci- dessous :

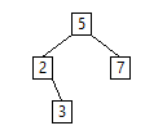
image

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
def insere(arbre, cle):
    """ arbre est une instance de la classe Arbre qui implémente
        un arbre binaire de recherche.
    """
    if ...:
        if ...:
            insere(arbre.fg, cle)
        else:
            arbre.fg = Arbre(cle)
    else:
        if ...:
            insere(arbre.fd, cle)
        else:
            arbre.fd = Arbre(cle)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
def insere(arbre, cle):
""" arbre est une instance de la classe Arbre qui implémente
    un arbre binaire de recherche.
"""
    if cle < arbre.v:
        if arbre.fg is not None:
            insere(arbre.fg, cle)
        else:
            arbre.fg = Arbre(cle)
    else:
        if arbre.fd is not None:
            insere(arbre.fd, cle)
        else:
            arbre.fd = Arbre(cle)

Tests :

>>> a = Arbre(5)
>>> insere(a, 2)
>>> insere(a, 7)
>>> insere(a, 3)
>>> parcours(a, [])
[2, 3, 5, 7]
>>> insere(a, 1)
>>> insere(a, 4)
>>> insere(a, 6)
>>> insere(a, 8)
>>> parcours(a, [])
[1, 2, 3, 4, 5, 6, 7, 8]

➡ Complétez le code sur Basthon

Exercice 26.1

Programmer la fonction multiplication, prenant en paramètres deux nombres entiers n1 et n2, et qui renvoie le produit de ces deux nombres.

Les seules opérations autorisées sont l’addition et la soustraction. 

>>> multiplication(3, 5)
15
>>> multiplication(-4, -8)
32
>>> multiplication(-2, 6)
-12
>>> multiplication(-2, 0)
0

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
def multiplication(n1, n2):
    # on se ramène d'abord au cas où n1 et n2 sont tous les deux positifs :
    if n1 < 0:
        return -multiplication(-n1, n2)
    if n2 < 0:
        return -multiplication(n1, -n2)

    resultat = 0
    for _ in range(n2):
        resultat += n1
    return resultat

➡ Rédigez votre code sur Basthon

Exercice 26.2

Recopier et compléter sous Python la fonction suivante en respectant la spécification. On ne recopiera pas les commentaires.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
def dichotomie(tab, x):
    """
    tab : tableau d’entiers trié dans l’ordre croissant
    x : nombre entier
    La fonction renvoie True si tab contient x et False sinon
    """
    debut = 0
    fin = len(tab) - 1
    while debut <= fin:
        m = ...
        if x == tab[m]:
            return ...
        if x > tab[m]:
            debut = m + 1
        else:
            fin = ...
    return ...

Exemples : 

>>> dichotomie([15, 16, 18, 19, 23, 24, 28, 29, 31, 33],28)
True
>>> dichotomie([15, 16, 18, 19, 23, 24, 28, 29, 31, 33],27)
False


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
def dichotomie(tab, x):
    """
    tab : tableau d’entiers trié dans l’ordre croissant
    x : nombre entier
    La fonction renvoie True si tab contient x et False sinon
    """
    debut = 0
    fin = len(tab) - 1
    while debut <= fin:
        m = (debut + fin) // 2
        if x == tab[m]:
            return True
        if x > tab[m]:
            debut = m + 1
        else:
            fin = m - 1
    return False

➡ Complétez le code sur Basthon

Exercice 27.1

Écrire une fonction recherche_min qui prend en paramètre un tableau de nombres non trié tab, et qui renvoie l'indice de la première occurrence du minimum de ce tableau. Les tableaux seront représentés sous forme de liste Python.

Exemples : 

>>> recherche_min([5])
0
>>> recherche_min([2, 4, 1])
2
>>> recherche_min([5, 3, 2, 2, 4])
2


1
2
3
4
5
6
def recherche_min(tab):
    indice_min = 0
    for i in range(len(tab)):
        if tab[i] < tab[indice_min]:
            indice_min = i
    return indice_min

➡ Rédigez votre code sur Basthon

Exercice 27.2

On considère la fonction separe ci-dessous qui prend en argument un tableau tab dont les éléments sont des 0 et des 1 et qui sépare les 0 des 1 en plaçant les 0 en début de tableau et les 1 à la suite.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
def separe(tab):
    gauche = 0
    droite = ...
    while gauche < droite :
        if tab[gauche] == 0 :
            gauche = ...
        else :
            tab[gauche], tab[droite] = ...
            droite = ...
    return tab

Compléter la fonction separe ci-dessus.

Exemples :

>>> separe([1, 0, 1, 0, 1, 0, 1, 0])
[0, 0, 0, 0, 1, 1, 1, 1]
>>> separe([1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0])
[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1]

Description d’étapes effectuées par la fonction separe sur le tableau ci-dessous : tab = [1, 0, 1, 0, 1, 0, 1, 0]

  • Etape 1 : on regarde la première case, qui contient un 1 : ce 1 va aller dans la seconde partie du tableau final et on l’échange avec la dernière case. Il est à présent bien positionné : on ne prend plus la dernière case en compte.
    tab = [0, 0, 1, 0, 1, 0, 1, 1]

  • Etape 2 : on regarde à nouveau la première case, qui contient maintenant un 0 : ce 0 va aller dans la première partie du tableau final et est bien positionné : on ne prend plus la première case en compte.
    tab = [0, 0, 1, 0, 1, 0, 1, 1]

  • Etape 3 : on regarde la seconde case, qui contient un 0 : ce 0 va aller dans la première partie du tableau final et est bien positionné : on ne prend plus la seconde case en compte.
    tab = [0, 0, 1, 0, 1, 0, 1, 1]

  • Etape 4 : on regarde la troisième case, qui contient un 1 : ce 1 va aller dans la seconde partie du tableau final et on l’échange avec l’avant-dernière case. Il est à présent bien positionné : on ne prend plus l’avant-dernière case en compte.
    tab = [0, 0, 1, 0, 1, 0, 1, 1]

Et ainsi de suite...

tab = [0, 0, 0, 0, 1, 1, 1, 1]

Compléter la fonction separe présentée à la page précédente

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
def separe(tab):
    gauche = 0
    droite = len(tab) - 1
    while gauche < droite :
        if tab[gauche] == 0 :
            gauche = gauche + 1
        else :
            tab[gauche], tab[droite] = tab[droite], tab[gauche]
            droite = droite - 1
    return tab

➡ Complétez le code sur Basthon

Exercice 28.1

Écrire une fonction qui prend en paramètre un tableau d'entiers non vide et qui renvoie la moyenne de ces entiers. La fonction est spécifiée ci-après et doit passer les assertions fournies. 

def moyenne (tab):
    '''
    moyenne(list) -> float
    Entrée : un tableau non vide d'entiers
    Sortie : nombre de type float
    Correspondant à la moyenne des valeurs présentes dans le
    tableau
    '''

assert moyenne([1]) == 1
assert moyenne([1, 2, 3, 4, 5, 6, 7]) == 4
assert moyenne([1, 2]) == 1.5


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def moyenne(tab):
    '''
    moyenne(list) -> float
    Entrée : un tableau non vide d'entiers
    Sortie : nombre de type float
    Correspondant à la moyenne des valeurs présentes dans le
    tableau
    '''
    somme = 0
    for elt in tab:
        somme += elt
    return somme / len(tab)

➡ Rédigez votre code sur Basthon

Exercice 28.2

Le but de l'exercice est de compléter une fonction qui détermine si une valeur est présente dans un tableau de valeurs triées dans l'ordre croissant.

L'algorithme traite le cas du tableau vide et il est écrit pour que la recherche dichotomique ne se fasse que dans le cas où la valeur est comprise entre les valeurs extrêmes du tableau.

On distingue les trois cas qui renvoient False en renvoyant False, 1 , False, 2 et False, 3.

Compléter l'algorithme de dichotomie donné ci-après.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def dichotomie(tab, x):
    """
    tab : tableau trié dans l’ordre croissant
    x : nombre entier
    La fonction renvoie True si tab contient x et False sinon
    """
    # cas du tableau vide
    if ...:
        return False, 1

    # cas où x n'est pas compris entre les valeurs extrêmes
    if (x < tab[0]) or ...:
        return False, 2

    debut = 0
    fin = len(tab) - 1
    while debut <= fin:
        m = ...
        if x == tab[m]:
            return ...
        if x > tab[m]:
            debut = m + 1
        else:
            fin = ...
    return ...

Exemples :

>>> dichotomie([15, 16, 18, 19, 23, 24, 28, 29, 31, 33],28)
True
>>> dichotomie([15, 16, 18, 19, 23, 24, 28, 29, 31, 33],27)
(False, 3)
>>> dichotomie([15, 16, 18, 19, 23, 24, 28, 29, 31, 33],1)
(False, 2)
>>> dichotomie([],28)
(False, 1)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def dichotomie(tab, x):
    """
    tab : tableau trié dans l’ordre croissant
    x : nombre entier
    La fonction renvoie True si tab contient x et False sinon
    """
    # cas du tableau vide
    if tab == []:
        return False, 1

    # cas où x n'est pas compris entre les valeurs extrêmes
    if (x < tab[0]) or (x > tab[-1]):
        return False, 2

    debut = 0
    fin = len(tab) - 1
    while debut <= fin:
        m = (debut + fin) // 2
        if x == tab[m]:
            return True
        if x > tab[m]:
            debut = m + 1
        else:
            fin = m - 1
    return False, 3

➡ Complétez le code sur Basthon

Exercice 29.1

Un arbre binaire est implémenté par la classe Arbre donnée ci-dessous. Les attributs fg et fd prennent pour valeurs des instances de la classe Arbre ou None.

class Arbre:
    def __init__(self, etiquette):
        self.v = etiquette
        self.fg = None
        self.fd = None

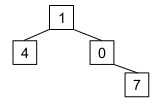
image

L’arbre ci-dessus sera donc implémenté de la manière suivante : 

a = Arbre(1)
a.fg = Arbre(4)
a.fd = Arbre(0)
a.fd.fd = Arbre(7)

Écrire une fonction récursive taille prenant en paramètre une instance a de la classe Arbre et qui renvoie la taille de l’arbre que cette instance implémente.

Écrire de même une fonction récursive hauteur prenant en paramètre une instance a de la classe Arbre et qui renvoie la hauteur de l’arbre que cette instance implémente.

Si un arbre a un seul nœud, sa taille et sa hauteur sont égales à 1. S’il est vide, sa taille et sa hauteur sont égales à 0.

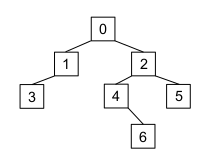
Tester les deux fonctions sur l’arbre représenté ci-dessous :

image

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
def taille(a):
    if a is None:
        return 0
    else:
        return 1 + taille(a.fg) + taille(a.fd)

def hauteur(a):
    if a is None:
        return 0
    else:
        return 1 + max(hauteur(a.fg), hauteur(a.fd))

Tests :

a = Arbre(0)
a.fg = Arbre(1)
a.fd = Arbre(2)
a.fg.fg = Arbre(3)
a.fd.fg = Arbre(4)
a.fd.fd = Arbre(5)
a.fd.fg.fd = Arbre(6)

>>> taille(a)
7
>>> hauteur(a)
4

➡ Rédigez votre code sur Basthon

Exercice 29.2

La méthode insert de la classe list permet d’insérer un élément dans une liste à un indice donné.

Le but de cet exercice est, sans utiliser cette méthode, d’écrire une fonction ajoute réalisant cette insertion en produisant une nouvelle liste.

Cette fonction ajoute prend en paramètres trois variables indice, element et liste et renvoie une liste L dans laquelle les éléments sont ceux de la liste liste avec, en plus, l’élément element à l’indice indice.
On considère que les variables indice et element sont des entiers positifs et que les éléments de liste sont également des entiers positifs.
Les éléments de la liste liste, dont les indices sont supérieurs ou égaux à indice apparaissent décalés vers la droite dans la liste L.
Si indice est supérieur ou égal au nombre d’éléments de la liste liste, l’élément element est ajouté dans L après tous les éléments de la liste liste.


Exemple : 

>>> ajoute(1, 4, [7, 8, 9])
[7, 4, 8, 9]
>>> ajoute(3, 4, [7, 8, 9])
[7, 8, 9, 4]
>>> ajoute(4, 4, [7, 8, 9])
[7, 8, 9, 4]

Compléter et tester le code ci-dessous :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
def ajoute(indice, element, liste):
    nbre_elts = len(liste)
    L = [0 for i in range(nbre_elts + 1)]
    if ...:
        for i in range(indice):
            L[i] = ...
        L[...] = ...
        for i in range(indice + 1, nbre_elts + 1):
            L[i] = ...
    else:
        for i in range(nbre_elts):
            L[i] = ...
        L[...] = ...
    return L

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
def ajoute(indice, element, liste):
    nbre_elts = len(liste)
    L = [0 for i in range(nbre_elts + 1)]
    if indice < nbre_elts:
        for i in range(indice):
            L[i] = liste[i]
        L[indice] = element
        for i in range(indice + 1, nbre_elts + 1):
            L[i] = liste[i-1]
    else:
        for i in range(nbre_elts):
            L[i] = liste[i]
        L[nbre_elts] = element 
    return L

➡ Complétez le code sur Basthon

Exercice 30.1

Écrire une fonction moyenne qui prend en paramètre un tableau non vide de nombres flottants et qui renvoie la moyenne des valeurs du tableau. Les tableaux seront représentés sous forme de liste Python.

Exemples : 

>>> moyenne([1.0])
1.0
>>> moyenne([1.0, 2.0, 4.0])
2.3333333333333335


1
2
3
4
5
def moyenne(tab):
    somme = 0
    for val in tab:
        somme += val
    return somme / len(tab)

➡ Rédigez votre code sur Basthon

Exercice 30.2

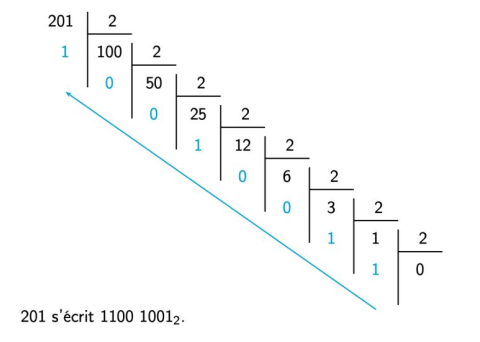
On considère la fonction binaire ci-dessous qui prend en paramètre un entier positif a en écriture décimale et qui renvoie son écriture binaire sous la forme d'une chaine de caractères.

L’algorithme utilise la méthode des divisions euclidiennes successives comme l’illustre l’exemple ci-après.

image

1
2
3
4
5
6
7
def binaire(a):
    bin_a = ...
    a = a // 2
    while a ... :
        bin_a = ... + bin_a
        a = ...
    return bin_a
Compléter le code de la fonction binaire.

Exemples : 

>>> binaire(83)
'1010011'
>>> binaire(127)
'1111111'
>>> binaire(0)
'0'


1
2
3
4
5
6
7
def binaire(a):
    bin_a = str(a%2)
    a = a // 2
    while a != 0 :
        bin_a = str(a%2) + bin_a
        a = a // 2
    return bin_a

➡ Complétez le code sur Basthon

Exercice 31.1

Écrire une fonction Python appelée nb_repetitions qui prend en paramètres un élément elt et une liste tab et renvoie le nombre de fois où l’élément apparaît dans la liste.

Exemples : 

>>> nb_repetitions(5, [2, 5, 3, 5, 6, 9, 5])
3
>>> nb_repetitions('A', ['B', 'A', 'B', 'A', 'R'])
2
>>> nb_repetitions(12, [1, '!', 7, 21, 36, 44])
0


1
2
3
4
5
6
def nb_repetitions(elt, tab):
    nb = 0
    for element in tab:
        if element == elt:
            nb += 1
    return nb

➡ Rédigez votre code sur Basthon

Exercice 31.2

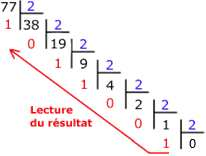
Pour rappel, la conversion d’un nombre entier positif en binaire peut s’effectuer à l’aide des divisions successives comme illustré ici :

image

Voici une fonction Python basée sur la méthode des divisions successives permettant de convertir un nombre entier positif en binaire :

1
2
3
4
5
6
7
def binaire(a):
    bin_a = str(...)
    a = a // 2
    while a ... :
        bin_a = ...(a%2) + ...
        a = ...
    return bin_a
Compléter la fonction binaire.

Exemples :

>>> binaire(0)
'0'
>>> binaire(77)
'1001101'

1
2
3
4
5
6
7
def binaire(a):
    bin_a = str(a%2)
    a = a // 2
    while a != 0 :
        bin_a = str(a%2) + bin_a
        a = a // 2
    return bin_a

➡ Complétez le code sur Basthon

Exercice 32.1

Écrire une fonction min_et_max qui prend en paramètre un tableau de nombres tab non vide, et qui renvoie la plus petite et la plus grande valeur du tableau sous la forme d’un dictionnaire à deux clés min et max.

Les tableaux seront représentés sous forme de liste Python.

L’utilisation des fonctions natives min, max et sorted, ainsi que la méthode sort n’est pas autorisée.

Exemples :

>>> min_et_max([0, 1, 4, 2, -2, 9, 3, 1, 7, 1])
{'min': -2, 'max': 9}
>>> min_et_max([0, 1, 2, 3])
{'min': 0, 'max': 3}
>>> min_et_max([3])
{'min': 3, 'max': 3}
>>> min_et_max([1, 3, 2, 1, 3])
{'min': 1, 'max': 3}
>>> min_et_max([-1, -1, -1, -1, -1])
{'min': -1, 'max': -1}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
def min_et_max(tab):
    d = {}
    d['min'] = tab[0]
    d['max'] = tab[0]
    for val in tab:
        if val < d['min']:
            d['min'] = val
        if val > d['max']:
            d['max'] = val
    return d

➡ Rédigez votre code sur Basthon

Exercice 32.2

On dispose d’une classe Carte permettant de créer des objets modélisant des cartes à jouer.

Compléter la classe Paquet_de_cartes suivante en respectant les spécifications données dans les chaînes de documentation.

Ajouter une assertion dans la méthode get_carte afin de vérifier que le paramètre pos est correct.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Carte:
    def __init__(self, c, v):
        """ Initialise les attributs couleur (entre 1 et 4), et valeur (entre 1 et 13). """
        self.couleur = c
        self.valeur = v

    def get_valeur(self):
        """ Renvoie la valeur de la carte : As, 2, ..., 10, Valet, Dame, Roi """
        valeurs = ['As','2', '3', '4', '5', '6', '7', '8', '9', '10', 'Valet', 'Dame', 'Roi']
        return valeurs[self.valeur - 1]

    def get_couleur(self):
        """ Renvoie la couleur de la carte (parmi pique, coeur, carreau, trèfle). """
        couleurs = ['pique', 'coeur', 'carreau', 'trèfle']
        return couleurs[self.couleur - 1]

class Paquet_de_cartes:
    def __init__(self):
        """ Initialise l'attribut contenu avec une liste des 52 objets Carte possibles
            rangés par valeurs croissantes en commençant par pique, puis coeur,
            carreau et tréfle. """
        # A compléter

    def get_carte(self, pos):
        """ Renvoie la carte qui se trouve à la position pos (entier compris entre 0 et 51). """
        # A compléter

Exemple :

Exemple :
>>> jeu = Paquet_de_cartes()
>>> carte1 = jeu.get_carte(20)
>>> print(carte1.get_valeur() + " de " + carte1.get_couleur())
8 de coeur
>>> carte2 = jeu.get_carte(0)
>>> print(carte2.get_valeur() + " de " + carte2.get_couleur())
As de pique
>>> carte3 = jeu.get_carte(52)
AssertionError : paramètre pos invalide

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Carte:
    def __init__(self, c, v):
        """ Initialise les attributs couleur (entre 1 et 4), et valeur (entre 1 et 13). """
        self.couleur = c
        self.valeur = v

    def get_valeur(self):
        """ Renvoie la valeur de la carte : As, 2, ..., 10, Valet, Dame, Roi """
        valeurs = ['As','2', '3', '4', '5', '6', '7', '8', '9', '10', 'Valet', 'Dame', 'Roi']
        return valeurs[self.valeur - 1]

    def get_couleur(self):
        """ Renvoie la couleur de la carte (parmi pique, coeur, carreau, trèfle). """
        couleurs = ['pique', 'coeur', 'carreau', 'trèfle']
        return couleurs[self.couleur - 1]

class Paquet_de_cartes:
    def __init__(self):
        """ Initialise l'attribut contenu avec une liste des 52 objets Carte possibles
            rangés par valeurs croissantes en commençant par pique, puis coeur,
            carreau et tréfle. """
        self.contenu = [Carte(c, v) for c in range(1, 5) for v in range(1, 14)]  

    def get_carte(self, pos):
        """ Renvoie la carte qui se trouve à la position pos (entier compris entre 0 et 51). """
        assert 0 <= pos <= 51,  'paramètre pos invalide'
        return self.contenu[pos]

➡ Complétez le code sur Basthon

Exercice 33.1

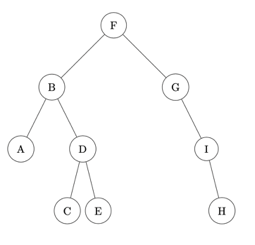
Dans cet exercice, un arbre binaire de caractères est stocké sous la forme d’un dictionnaire où les clefs sont les caractères des nœuds de l’arbre et les valeurs, pour chaque clef, la liste des caractères des fils gauche et droit du nœud.

Par exemple, l’arbre

image

est stocké dans

a = {'F':['B','G'], 'B':['A','D'], 'A':['',''], 'D':['C','E'], \
'C':['',''], 'E':['',''], 'G':['','I'], 'I':['','H'], \
'H':['','']}

Écrire une fonction récursive taille prenant en paramètres un arbre binaire arbre sous la forme d’un dictionnaire et un caractère lettre qui est la valeur du sommet de l’arbre, et qui renvoie la taille de l’arbre à savoir le nombre total de nœuds.

On observe que, par exemple, arbre[lettre][0], respectivement arbre[lettre][1], permet d’atteindre la clé du sous-arbre gauche, respectivement droit, de l’arbre arbre de sommet lettre.

Exemple : 

>>> taille(a, ’F’)
9


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
a = {'F':['B','G'], 'B':['A','D'], 'A':['',''], 'D':['C','E'], 'C':['',''], 'E':['',''], 'G':['','I'], 'I':['','H'], 'H':['','']}

def taille(arbre, lettre):
    fils_gauche = arbre[lettre][0]
    fils_droit = arbre[lettre][1]

    if fils_gauche != '' and fils_droit != '':
        return 1 + taille(arbre, fils_gauche) + taille(arbre, fils_droit)

    if fils_gauche != '' and fils_droit == '':
        return 1 + taille(arbre, fils_gauche)

    if fils_gauche == '' and fils_droit != '':
        return 1 + taille(arbre, fils_droit)

    else:
        return 1

ou plus simplement :

1
2
3
4
def taille(arbre, lettre):
    if lettre == '':
        return 0
    return 1 + taille(arbre, arbre[lettre][0]) + taille(arbre, arbre[lettre][1])

➡ Rédigez votre code sur Basthon

Exercice 33.2

On considère l'algorithme de tri de tableau suivant : à chaque étape, on parcourt le sous- tableau des éléments non rangés et on place le plus petit élément en première position de ce sous-tableau.

Exemple avec le tableau : t = [41, 55, 21, 18, 12, 6, 25]

  • Étape 1 : on parcourt tous les éléments du tableau, on permute le plus petit élément avec le premier. Le tableau devient t = [6, 55, 21, 18, 12, 41, 25]

  • Étape 2 : on parcourt tous les éléments sauf le premier, on permute le plus petit élément trouvé avec le second. Le tableau devient : t = [6, 12, 21, 18, 55, 41, 25]

Et ainsi de suite.

La code de la fonction tri_selection qui implémente cet algorithme est donné ci- dessous.

1
2
3
4
5
6
7
8
def tri_selection(tab):
    N = len(tab)
    for k in range(...):
        imin = ...
        for i in range(... , N):
            if tab[i] < ... :
                imin = i
        ... , tab[imin] = tab[imin] , ...

Compléter le code de cette fonction de façon à obtenir :

>>> liste = [41, 55, 21, 18, 12, 6, 25]
>>> tri_selection(liste)
>>> liste
[6, 12, 18, 21, 25, 41, 55]

On rappelle que l'instruction a, b = b, a échange les contenus de a et de b.

1
2
3
4
5
6
7
8
def tri_selection(tab):
    N = len(tab)
    for k in range(N):
        imin = k
        for i in range(k, N):
            if tab[i] < tab[imin] :
                imin = i
        tab[k] , tab[imin] = tab[imin] , tab[k]

➡ Complétez le code sur Basthon

Exercice 34.1

Programmer la fonction moyenne prenant en paramètre un tableau d'entiers tab (de type list) qui renvoie la moyenne de ses éléments si le tableau est non vide. Proposer une façon de traiter le cas où le tableau passé en paramètre est vide.

Dans cet exercice, on s’interdira d’utiliser la fonction Python sum.

Exemples : 

>>> moyenne([5,3,8])
5.333333333333333
>>> moyenne([1,2,3,4,5,6,7,8,9,10])
5.5
>>> moyenne([])
# Comportement différent suivant le traitement proposé.


1
2
3
4
5
6
7
8
9
def moyenne(tab):
    if tab == []:
        print('Le tableau donné est vide')
        return None
    else:
        somme = 0
        for elt in tab:
            somme += elt
        return somme / len(tab)

➡ Rédigez votre code sur Basthon

Exercice 34.2

On considère un tableau d'entiers tab (de type list) dont les éléments sont des 0 ou des 1). On se propose de trier ce tableau selon l'algorithme suivant : à chaque étape du tri, le tableau est constitué de trois zones consécutives, la première ne contenant que des 0, la seconde n'étant pas triée et la dernière ne contenant que des 1.

Zone de 0Zone non triéeZone de 1

Tant que la zone non triée n'est pas réduite à un seul élément, on regarde son premier élément :

  • si cet élément vaut 0, on considère qu'il appartient désormais à la zone ne contenant que des 0 ;
  • si cet élément vaut 1, il est échangé avec le dernier élément de la zone non triée et on considère alors qu’il appartient à la zone ne contenant que des 1.

Dans tous les cas, la longueur de la zone non triée diminue de 1.

Recopier sous Python en la complétant la fonction tri suivante :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
def tri(tab):
    # i est le premier indice de la zone non triée,
    # j est le dernier indice de cette zone non triée.
    # Au début, la zone non triée est le tableau complet.
    i = ...
    j = ...
    while i != j:
        if tab[i]== 0:
            i = ...
        else:
            valeur = tab[j]
            tab[j] = ...
            ...
            j = ...
    ...

Exemple : 

>>> tri([0,1,0,1,0,1,0,1,0])
[0, 0, 0, 0, 0, 1, 1, 1, 1]       


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
def tri(tab):
    # i est le premier indice de la zone non triée,
    # j est le dernier indice de cette zone non triée.
    # Au début, la zone non triée est le tableau complet.
    i = 0
    j = len(tab) - 1
    while i != j :
        if tab[i] == 0:
            i = i + 1
        else :
            valeur = tab[j]
            tab[j] = tab[i]
            tab[i] = valeur
            j = j - 1
    return tab

➡ Complétez le code sur Basthon

Exercice 35.1

L'opérateur « ou exclusif » entre deux bits renvoie 0 si les deux bits sont égaux et 1 s'ils sont différents. Il est symbolisé par le caractère ⊕. Ainsi :

  • 0 ⊕ 0 = 0
  • 0 ⊕ 1 = 1
  • 1 ⊕ 0 = 1
  • 1 ⊕ 1 = 0

On représente ici une suite de bits par un tableau contenant des 0 et des 1.

Exemples :

a = [1, 0, 1, 0, 1, 1, 0, 1]
b = [0, 1, 1, 1, 0, 1, 0, 0]
c = [1, 1, 0, 1]
d = [0, 0, 1, 1]

Écrire la fonction ou_exclusif qui prend en paramètres deux tableaux de même longueur et qui renvoie un tableau où l’élément situé à position i est le résultat, par l’opérateur « ou exclusif », des éléments à la position i des tableaux passés en paramètres.

En considérant les quatre exemples ci-dessus, cette fonction donne :

>>> ou_exclusif(a, b)
[1, 1, 0, 1, 1, 0, 0, 1])
>>> ou_exclusif(c, d)
[1, 1, 1, 0]

1
2
3
4
5
6
def ou_exclusif(tab1, tab2):
    resultat = []
    taille = len(tab1)
    for i in range(taille):
        resultat.append(tab1[i] ^ tab2[i])
    return resultat

Si on ne connait pas la fonction native ^ qui fait le «ou exclusif» de deux entiers en Python, on peut la recoder :

1
2
3
4
5
6
7
8
9
def ou_exc(a, b):
    if a == 0 and b == 0:
        return 0
    if a == 0 and b == 1:
        return 1
    if a == 1 and b == 0:
        return 1
    if a == 1 and b == 1:
        return 0

Le code devient alors :

1
2
3
4
5
6
def ou_exclusif(tab1, tab2):
    resultat = []
    taille = len(tab1)
    for i in range(taille):
        resultat.append(ou_exc(tab1[i],tab2[i]))
    return resultat

➡ Rédigez votre code sur Basthon

Exercice 35.2

Dans cet exercice, on appelle carré d’ordre \(n\) un tableau de \(n\) lignes et \(n\) colonnes dont chaque case contient un entier naturel.

Exemples : image

Un carré est dit semimagique lorsque les sommes des éléments situés sur chaque ligne, chaque colonne sont égales.

  • Ainsi c2 et c3 sont semimagiques car la somme de chaque ligne, chaque colonne et chaque diagonale est égale à 8 pour c2 et 12 pour c3.

  • Le carre c3bis n'est pas semimagique car la somme de la première ligne est égale à 15 alors que celle de la deuxième ligne est égale à 10.

La classe Carre ci-après contient des méthodes qui permettent de manipuler des carrés.

  • La méthode constructeur crée un carré sous forme d’un tableau à deux dimensions à partir d’une liste d’entiers, et d’un ordre.

  • La méthode affiche permet d’afficher le carré créé.

Exemple :

>>> liste = (3, 4, 5, 4, 4, 4, 5, 4, 3)
>>> c3 = Carre(liste, 3)
>>> c3.affiche()
[3, 4, 5]
[4, 4, 4]
[5, 4, 3]

Compléter la méthode est_semimagique qui renvoie True si le carré est semimagique, False sinon. Puis tester la fonction est_semimagique sur les carrés c2, c3 et c3bis.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Carre:
    def __init__(self, liste, n):
        self.ordre = n
        self.tableau = [[liste[i + j * n] for i in range(n)] for j in range(n)]

    def affiche(self):
        '''Affiche un carré'''
        for i in range(self.ordre):
            print(self.tableau[i])

    def somme_ligne(self, i):
        '''Calcule la somme des valeurs de la ligne i'''
        somme = 0
        for j in range(self.ordre):
            somme = somme + self.tableau[i][j]
        return somme

    def somme_col(self, j):
        '''Calcule la somme des valeurs de la colonne j'''
        somme = 0
        for i in range(self.ordre):
            somme = somme + self.tableau[i][j]
        return somme

    def est_semimagique(self):
        s = self.somme_ligne(0)

        #test de la somme de chaque ligne
        for i in range(...):
            if ... != s:
                return ...

        #test de la somme de chaque colonne
        for j in range(...):
            if ... != s:
                return ...

        return ...

Listes permettant de générer les carrés c2, c3 et c3bis :

1
2
3
lst_c2 = [1, 7, 7, 1]
lst_c3 = [3, 4, 5, 4, 4, 4, 5, 4, 3]
lst_c3bis = [2, 9, 4, 7, 0, 3, 6, 1, 8]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Carre:
    def __init__(self, liste, n):
        self.ordre = n
        self.tableau = [[liste[i + j * n] for i in range(n)] for j in range(n)]

    def affiche(self):
        '''Affiche un carré'''
        for i in range(self.ordre):
            print(self.tableau[i])

    def somme_ligne(self, i):
        '''Calcule la somme des valeurs de la ligne i'''
        somme = 0
        for j in range(self.ordre):
            somme = somme + self.tableau[i][j]
        return somme

    def somme_col(self, j):
        '''Calcule la somme des valeurs de la colonne j'''
        somme = 0
        for i in range(self.ordre):
            somme = somme + self.tableau[i][j]
        return somme

    def est_semimagique(self):
        s = self.somme_ligne(0)

        #test de la somme de chaque ligne
        for i in range(self.ordre):
            if self.somme_ligne(i) != s:
                return False

        #test de la somme de chaque colonne
        for j in range(self.ordre):
            if self.somme_col(j) != s:
                return False

        return True

Tests avec :

1
2
3
lst_c2 = [1, 7, 7, 1]
lst_c3 = [3, 4, 5, 4, 4, 4, 5, 4, 3]
lst_c3bis = [2, 9, 4, 7, 0, 3, 6, 1, 8]

>>> c2 = Carre(lst_c2, 2)
>>> c2.est_semimagique()
True

>>> c3 = Carre(lst_c3, 3)
>>> c3.est_semimagique()
True

>>> c3bis = Carre(lst_c3bis, 2)
>>> c3bis.est_semimagique()
False

➡ Complétez le code sur Basthon

Exercice 36.1

Écrire une fonction couples_consecutifs qui prend en paramètre une liste de nombres entiers tab non vide, et qui renvoie la liste (éventuellement vide) des couples d'entiers consécutifs successifs qu'il peut y avoir dans tab.

Exemples : 

>>> couples_consecutifs([1, 4, 3, 5])
[]
>>> couples_consecutifs([1, 4, 5, 3])
[(4, 5)]
>>> couples_consecutifs([1, 1, 2, 4])
[(1, 2)]
>>> couples_consecutifs([7, 1, 2, 5, 3, 4])
[(1, 2), (3, 4)]
>>> couples_consecutifs([5, 1, 2, 3, 8, -5, -4, 7])
[(1, 2), (2, 3), (-5, -4)]


1
2
3
4
5
6
def couples_consecutifs(tab):
    solution = []
    for i in range(len(tab)-1):
        if tab[i] + 1 == tab[i+1]:
            solution.append((tab[i], tab[i+1]))
    return solution

➡ Rédigez votre code sur Basthon

Exercice 36.2

Soit une image binaire représentée dans un tableau à 2 dimensions. Les éléments M[i][j], appelés pixels, sont égaux soit à 0 soit à 1.

Une composante d’une image est un sous-ensemble de l’image constitué uniquement de 1 et de 0 qui sont côte à côte, soit horizontalement soit verticalement.

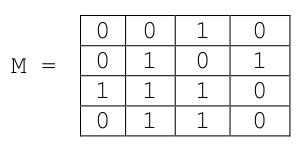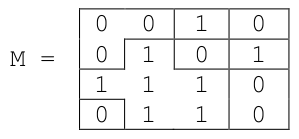
Par exemple, les composantes de image sont image

On souhaite, à partir d’un pixel égal à 1 dans une image M, donner la valeur val à tous les pixels de la composante à laquelle appartient ce pixel.

La fonction propager prend pour paramètre une image M (représentée par une liste de listes), deux entiers i et j et unevaleur entière val. Elle met à la valeur val tous les pixels de la composante du pixel M[i][j] s’il vaut 1 et ne fait rien s’il vaut 0.

Par exemple, propager(M, 2, 1, 3) donne ![image]((!!sujets/term/pratique/img/36_carre3_png){: .center width=30%}

Compléter le code récursif de la fonction propager donné ci-dessous :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
def propager(M, i, j, val):
    if M[i][j] == ...:
        M[i][j] = val

    # l'element en haut fait partie de la composante
    if i-1 >= 0 and M[i-1][j] == ...:
        propager(M, i-1, j, val)

    # l'element en bas fait partie de la composante
    if ... < len(M) and M[i+1][j] == 1:
        propager(M, ..., j, val)

    # l'element à gauche fait partie de la composante
    if ... and M[i][j-1] == 1:
        propager(M, ..., ..., val)

    # l'element à droite fait partie de la composante
    if ... and ...:
        propager(..., ..., ..., ...)

Exemple : 

>>> M = [[0, 0, 1, 0], [0, 1, 0, 1], [1, 1, 1, 0], [0, 1, 1, 0]]
>>> propager(M, 2, 1, 3)
>>> M
[[0, 0, 1, 0], [0, 3, 0, 1], [3, 3, 3, 0], [0, 3, 3, 0]]


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
def propager(M, i, j, val):
    if M[i][j] == 1:
        M[i][j] = val

    # l'element en haut fait partie de la composante
    if i-1 >= 0 and M[i-1][j] == 1:
        propager(M, i-1, j, val)

    # l'element en bas fait partie de la composante
    if i+1 < len(M) and M[i+1][j] == 1:
        propager(M, i+1, j, val)

    # l'element à gauche fait partie de la composante
    if j-1 >= 0 and M[i][j-1] == 1:
        propager(M, i, j-1, val)

    # l'element à droite fait partie de la composante
    if j+1 < len(M[i]) and M[i][j+1] == 1:
        propager(M, i, j+1, val)

➡ Complétez le code sur Basthon

Exercice 37.1

Écrire une fonction recherche qui prend en paramètres elt un nombre entier et tab un tableau de nombres entiers, et qui renvoie l’indice de la dernière occurrence de elt dans tab si elt est dans tab et -1 sinon.

Exemples : 

>>> recherche(1, [2, 3, 4])
-1
>>> recherche(1, [10, 12, 1, 56])
2
>>> recherche(1, [1, 0, 42, 7])
0
>>> recherche(1, [1, 50, 1])
2
>>> recherche(1, [8, 1, 10, 1, 7, 1, 8])
5


1
2
3
4
5
def recherche(elt, tab):
    for i in range(len(tab)-1, -1, -1):
        if tab[i] == elt:
            return i
    return -1

➡ Rédigez votre code sur Basthon

Exercice 37.2

On définit une classe gérant une adresse IPv4.

On rappelle qu’une adresse IPv4 est une adresse de longueur 4 octets, notée en décimale à point, en séparant chacun des octets par un point. On considère un réseau privé avec une plage d’adresses IP de 192.168.0.0 à 192.168.0.255.

On considère que les adresses IP saisies sont valides.

Les adresses IP 192.168.0.0 et 192.168.0.255 sont des adresses réservées.

Le code ci-dessous implémente la classe AdresseIP.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class AdresseIP:
    def __init__(self, adresse):
        self.adresse = ...

    def liste_octet(self):
        """renvoie une liste de nombres entiers,
        la liste des octets de l'adresse IP"""
        return [int(i) for i in self.adresse.split(".")]

    def est_reservee(self):
        """renvoie True si l'adresse IP est une adresse
        réservée, False sinon"""
        return ... or ...

    def adresse_suivante(self):
        """renvoie un objet de AdresseIP avec l'adresse
        IP qui suit l’adresse self
        si elle existe et False sinon"""
        if ... < 254:
            octet_nouveau = ... + ...
            return AdresseIP('192.168.0.' + ...)
        else:
            return False
Compléter le code ci-dessus et instancier trois objets : adresse1, adresse2, adresse3 avec respectivement les arguments suivants :

'192.168.0.1', '192.168.0.2', '192.168.0.0'

Vérifier que : 

>>> adresse1.est_reservee()
False
>>> adresse3.est_reservee()
True
>>> adresse2.adresse_suivante().adresse
'192.168.0.3'


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class AdresseIP:
    def __init__(self, adresse):
        self.adresse = adresse

    def liste_octet(self):
        """renvoie une liste de nombres entiers,
        la liste des octets de l'adresse IP"""
        return [int(i) for i in self.adresse.split(".")]

    def est_reservee(self):
        """renvoie True si l'adresse IP est une adresse
        réservée, False sinon"""
        return self.liste_octet()[3] == 0 or self.liste_octet()[3] == 255

    def adresse_suivante(self):
        """renvoie un objet de AdresseIP avec l'adresse
        IP qui suit l’adresse self
        si elle existe et False sinon"""
        if self.liste_octet()[3] < 254:
            octet_nouveau = self.liste_octet()[3] + 1
            return AdresseIP('192.168.0.' + str(octet_nouveau))
        else:
            return False

adresse1 = AdresseIP('192.168.0.1')
adresse2 = AdresseIP('192.168.0.2')
adresse3 = AdresseIP('192.168.0.0')

➡ Complétez le code sur Basthon

Exercice 38.1

On considère des mots à trous : ce sont des chaînes de caractères contenant uniquement des majuscules et des caractères *. Par exemple INFO*MA*IQUE, ***I***E** et *S* sont des mots à trous.

Programmer une fonction correspond qui :

  • prend en paramètres deux chaînes de caractères mot et mot_a_trous où mot_a_trous est un mot à trous comme indiqué ci-dessus,
  • renvoie :
    • True si on peut obtenir mot en remplaçant convenablement les caractères '*' de mot_a_trous.
    • False sinon.

Exemple :

>>> correspond('INFORMATIQUE', 'INFO*MA*IQUE')
True
>>> correspond('AUTOMATIQUE', 'INFO*MA*IQUE')
False
>>> correspond('STOP', 'S*')
False
>>> correspond('AUTO', '*UT*')
True

1
2
3
4
5
6
7
def correspond(mot, mot_a_trous):
    if len(mot) != len(mot_a_trous):
        return False
    for i in range(len(mot)):
        if mot[i] != mot_a_trous[i] and mot_a_trous[i] != '*':
            return False
    return True

➡ Rédigez votre code sur Basthon

Exercice 38.2

On considère au plus 26 personnes A, B, C, D, E, F ... qui peuvent s'envoyer des messages avec deux règles à respecter :

  • chaque personne ne peut envoyer des messages qu'à une seule personne (éventuellement elle-même),
  • chaque personne ne peut recevoir des messages qu'en provenance d'une seule personne (éventuellement elle-même).

Voici un exemple - avec 6 personnes - de « plan d'envoi des messages » qui respecte les règles ci-dessus, puisque chaque personne est présente une seule fois dans chaque colonne :

  • A envoie ses messages à E
  • E envoie ses messages à B
  • B envoie ses messages à F
  • F envoie ses messages à A
  • C envoie ses messages à D
  • D envoie ses messages à C

Et le dictionnaire correspondant à ce plan d'envoi est le suivant :

plan_a = {'A':'E', 'B':'F', 'C':'D', 'D':'C', 'E':'B', 'F':'A'}

Un cycle est une suite de personnes dans laquelle la dernière est la même que la première.

Sur le plan d'envoi plan_a des messages ci-dessus, il y a deux cycles distincts : un premier cycle avec A, E, B, F et un second cycle avec C et D.

En revanche, le plan d’envoi plan_b ci-dessous :

plan_b = {'A':'C', 'B':'F', 'C':'E', 'D':'A', 'E':'B', 'F':'D'}

comporte un unique cycle : A, C, E, B, F, D. Dans ce cas, lorsqu’un plan d’envoi comporte un unique cycle, on dit que le plan d’envoi est cyclique.

Pour savoir si un plan d'envoi de messages comportant N personnes est cyclique, on peut utiliser l'algorithme ci-dessous :

  • on part d’un expéditeur (ici A) et on inspecte son destinataire dans le plan d'envoi,
  • chaque destinataire devient à son tour expéditeur, selon le plan d’envoi, tant qu’on ne « retombe » pas sur l’expéditeur initial,
  • le plan d’envoi est cyclique si on l’a parcouru en entier.

Compléter la fonction est_cyclique en respectant la spécification.

Remarque : la fonction python len permet d'obtenir la longueur d'un dictionnaire.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
def est_cyclique(plan):
    '''
    Prend en paramètre un dictionnaire `plan` correspondant à un plan d'envoi de messages (ici entre les personnes A, B, C, D, E, F).
    Renvoie True si le plan d'envoi de messages est cyclique et False sinon.
    '''
    expediteur = 'A'
    destinataire = plan[ ... ]
    nb_destinaires = 1

    while destinataire != ...:
        destinataire = plan[ ... ]
        nb_destinaires += ...

    return nb_destinaires == ...

Exemples :

>>> est_cyclique({'A':'E', 'F':'A', 'C':'D', 'E':'B', 'B':'F', 'D':'C'})
False
>>> est_cyclique({'A':'E', 'F':'C', 'C':'D', 'E':'B', 'B':'F', 'D':'A'})
True
>>> est_cyclique({'A':'B', 'F':'C', 'C':'D', 'E':'A', 'B':'F', 'D':'E'})
True
>>> est_cyclique({'A':'B', 'F':'A', 'C':'D', 'E':'C', 'B':'F', 'D':'E'})
False

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
def est_cyclique(plan):
    '''
    Prend en paramètre un dictionnaire `plan` correspondant à un plan d'envoi de messages (ici entre les personnes A, B, C, D, E, F).
    Renvoie True si le plan d'envoi de messages est cyclique et False sinon.
    '''
    expediteur = 'A'
    destinataire = plan[expediteur]
    nb_destinaires = 1

    while destinataire != expediteur:
        destinataire = plan[destinataire]
        nb_destinaires += 1

    return nb_destinaires == len(plan)

#tests
print(est_cyclique({'A':'E', 'F':'A', 'C':'D', 'E':'B', 'B':'F', 'D':'C'}))
print(est_cyclique({'A':'E', 'F':'C', 'C':'D', 'E':'B', 'B':'F', 'D':'A'}))
print(est_cyclique({'A':'B', 'F':'C', 'C':'D', 'E':'A', 'B':'F', 'D':'E'}))
print(est_cyclique({'A':'B', 'F':'A', 'C':'D', 'E':'C', 'B':'F', 'D':'E'}))

➡ Complétez le code sur Basthon

Exercice 39.1

On s’intéresse à la suite d’entiers définie par :

  • les deux premiers termes sont égaux à 1,
  • ensuite, chaque terme est obtenu en faisant la somme des deux termes qui le précèdent.

En mathématiques, on le formule ainsi :

\(U_1 = 1\), \(U_2 = 1\) et, pour tout entier naturel non nul \(n\), par \(U_{n+2} = U_{n+1} + U_n\).

Cette suite est connue sous le nom de suite de Fibonacci.
Écrire en Python une fonction fibonacci qui prend en paramètre un entier n supposé strictement positif et qui renvoie le terme d’indice n de cette suite.

Exemples :

>>> fibonacci(1)
1
>>> fibonacci(2)
1
>>> fibonacci(25)
75025
>>> fibonacci(45)
1134903170

Version récursive :

1
2
3
4
5
6
7
def fibonacci(n):
    if n == 0 :
        return 0   
    elif n == 1 :
        return 1
    else :
        return fibonacci(n-1) + fibonacci(n-2)

Version impérative : 

1
2
3
4
5
6
7
8
def fibonacci(n):
    a = 0
    b = 1
    for k in range(n-1):
        t = b
        b = a + b
        a = t
    return b

Version programmation dynamique :

1
2
3
4
5
6
7
def fibonacci(n):
    d = {}
    d[1] = 1
    d[2] = 1
    for k in range(3, n+1):
        d[k] = d[k-1] + d[k-2]
    return d[n]

➡ Rédigez votre code sur Basthon

Exercice 39.2

On considère la fonction pantheon prenant en paramètres eleves et notes deux tableaux de même longueur, le premier contenant le nom des élèves et le second, des entiers positifs désignant leur note à un contrôle de sorte que eleves[i] a obtenu la note notes[i].
Cette fonction renvoie le couple constitué de la note maximale attribuée et des noms des élèves ayant obtenu cette note regroupés dans un tableau.
Ainsi, l’instruction pantheon(['a', 'b', 'c', 'd'], [15, 18, 12, 18]) renvoie le couple (18, ['b', 'd']).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def pantheon(eleves, notes):
    note_maxi = 0
    meilleurs_eleves =  ...

    for i in range(...) :
        if notes[i] == ... :
            meilleurs_eleves.append(...)
        elif notes[i] > note_maxi:
            note_maxi = ...
            meilleurs_eleves = [...]

    return (note_maxi,meilleurs_eleves)

Compléter ce code.

Exemples :

>>> eleves_nsi = ['a','b','c','d','e','f','g','h','i','j']
>>> notes_nsi = [30, 40, 80, 60, 58, 80, 75, 80, 60, 24]
>>> pantheon(eleves_nsi, notes_nsi)
(80, ['c', 'f', 'h'])
>>> pantheon([],[])
(0, [])

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def pantheon(eleves, notes):
    note_maxi = 0
    meilleurs_eleves =  []

    for i in range(len(eleves)) :
        if notes[i] == note_maxi :
            meilleurs_eleves.append(eleves[i])
        elif notes[i] > note_maxi:
            note_maxi = notes[i]
            meilleurs_eleves = [i]

    return (note_maxi, meilleurs_eleves)

➡ Complétez le code sur Basthon

Exercice 40.1

Pour cet exercice :

  • On appelle « mot » une chaîne de caractères composée avec des caractères choisis parmi les 26 lettres minuscules ou majuscules de l'alphabet,

  • On appelle « phrase » une chaîne de caractères :

    • composée avec un ou plusieurs « mots » séparés entre eux par un seul caractère espace ' ',
    • se finissant :
      • soit par un point '.' qui est alors collé au dernier mot,
      • soit par un point d'exclamation '!' ou d'interrogation '?' qui est alors séparé du dernier mot par un seul caractère espace ' '.

Exemples :

  • 'Cet exercice est simple.'
  • 'Le point d exclamation est separe !'

Après avoir remarqué le lien entre le nombre de mots et le nombres de caractères espace dans une phrase, programmer une fonction nombre_de_mots qui prend en paramètre une phrase et renvoie le nombre de mots présents dans cette phrase.

>>> nombre_de_mots('Le point d exclamation est separe !')
6
>>> nombre_de_mots('Il y a un seul espace entre les mots !')
9
>>> nombre_de_mots('Combien de mots y a t il dans cette phrase ?')
10
>>> nombre_de_mots('Fin.')
1

1
2
3
4
5
6
def nombre_de_mots(phrase):
    nb_mots = 0
    for caractere in phrase:
        if caractere == ' ' or caractere == '.':
            nb_mots += 1
    return nb_mots

➡ Rédigez votre code sur Basthon

Exercice 40.2

La classe ABR ci-dessous permet d'implémenter une structure d'arbre binaire de recherche.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Noeud:
    def __init__(self, valeur):
        '''Méthode constructeur pour la classe Noeud.
        Paramètre d'entrée : valeur (str)'''
        self.valeur = valeur
        self.gauche = None
        self.droit = None

    def getValeur(self):
        '''Méthode accesseur pour obtenir la valeur du noeud
        Aucun paramètre en entrée'''
        return self.valeur

    def droitExiste(self):
        '''Méthode renvoyant True si l'enfant droit existe
        Aucun paramètre en entrée'''
        return (self.droit is not None)

    def gaucheExiste(self):
        '''Méthode renvoyant True si l'enfant gauche existe
        Aucun paramètre en entrée'''
        return (self.gauche is not None)

    def inserer(self, cle):
        '''Méthode d'insertion de clé dans un arbre binaire de recherche
        Paramètre d'entrée : cle (int)'''
        if cle < ...:
            # on insère à gauche
            if self.gaucheExiste():
                # on descend à gauche et on retente l'insertion de la clé
                ...
            else:
                # on crée un fils gauche
                self.gauche = ...
        elif cle > ... :
            # on insère à droite
            if ... :
                # on descend à droite et on retente l'insertion de la clé
                ...
            else:
                # on crée un fils droit
                ... = Noeud(cle)

Compléter la fonction récursive inserer afin qu'elle permette d’insérer un nœud dans l’arbre binaire de recherche proposé, à l’aide de sa clé.

Voici un exemple d'utilisation :

>>> arbre = Noeud(7)
>>> for cle in (3, 9, 1, 6):
        arbre.inserer(cle)
>>> arbre.gauche.getValeur()
3
>>> arbre.droit.getValeur()
9
>>> arbre.gauche.gauche.getValeur()
1
>>> arbre.gauche.droit.getValeur()
6

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Noeud:
    def __init__(self, valeur):
        '''Méthode constructeur pour la classe Noeud.
        Paramètre d'entrée : valeur (str)'''
        self.valeur = valeur
        self.gauche = None
        self.droit = None

    def getValeur(self):
        '''Méthode accesseur pour obtenir la valeur du noeud
        Aucun paramètre en entrée'''
        return self.valeur

    def droitExiste(self):
        '''Méthode renvoyant True si l'enfant droit existe
        Aucun paramètre en entrée'''
        return (self.droit is not None)

    def gaucheExiste(self):
        '''Méthode renvoyant True si l'enfant gauche existe
        Aucun paramètre en entrée'''
        return (self.gauche is not None)

    def inserer(self, cle):
        '''Méthode d'insertion de clé dans un arbre binaire de recherche
        Paramètre d'entrée : cle (int)'''
        if cle < self.valeur:
            # on insère à gauche
            if self.gaucheExiste():
                # on descend à gauche et on retente l'insertion de la clé
                self.gauche.inserer(cle)
            else:
                # on crée un fils gauche
                self.gauche = Noeud(cle)
        elif cle > self.valeur:
            # on insère à droite
            if self.droitExiste():
                # on descend à droite et on retente l'insertion de la clé
                self.droit.inserer(cle)
            else:
                # on crée un fils droit
                self.droit = Noeud(cle)

➡ Complétez le code sur Basthon

Exercice 41.1

Écrire une fonction recherche(caractere, chaine) qui prend en paramètres caractere, un unique caractère (c’est-à-dire une chaîne de caractère de longueur 1), et chaine, une chaîne de caractères. Cette fonction renvoie le nombre d’occurrences de caractere dans chaine, c’est-à-dire le nombre de fois où caractere apparaît dans chaine.

Exemples : 

>>> recherche('e', "sciences")
2
>>> recherche('i',"mississippi")
4
>>> recherche('a',"mississippi")
0


1
2
3
4
5
6
def recherche(caractere, chaine):
    somme = 0
    for lettre in chaine:
        if lettre == caractere:
            somme += 1
    return somme

➡ Rédigez votre code sur Basthon

Exercice 41.2

On s’intéresse à un algorithme récursif qui permet de rendre la monnaie à partir d’une liste donnée de valeurs de pièces et de billets.

Le système monétaire est donné sous forme d’une liste valeurs = [100, 50, 20, 10, 5, 2, 1]. On suppose que les pièces et billets sont disponibles sans limitation.

On cherche à donner la liste des valeurs à rendre pour une somme donnée en argument. L’algorithme utilisé est de type glouton.

Compléter le code Python ci-dessous de la fonction rendu_glouton qui implémente cet algorithme et renvoie la liste des pièces à rendre.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
valeurs = [100, 50, 20, 10, 5, 2, 1]

def rendu_glouton(a_rendre, rang):
    if a_rendre == 0:
        return ...
    v = valeurs[rang]
    if v <= ... :
        return ... + rendu_glouton(a_rendre - v, rang)
    else :
        return rendu_glouton(a_rendre, ...)

On devra obtenir :

>>>rendu_glouton(67, 0)
[50, 10, 5, 2]
>>>rendu_glouton(291, 0)
[100, 100, 50, 20, 20, 1]
>>> rendu_glouton(291,1) # si on ne dispose pas de billets de 100
[50, 50, 50, 50, 50, 20, 20, 1]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
valeurs = [100,50,20,10,5,2,1]

def rendu_glouton(a_rendre, rang):
    if a_rendre == 0:
        return []
    v = valeurs[rang]
    if v <= a_rendre :
        return [v] + rendu_glouton(a_rendre - v, rang)
    else :
        return rendu_glouton(a_rendre, rang + 1)

➡ Complétez le code sur Basthon

Exercice 42.1

Écrire une fonction tri_selection qui prend en paramètre une liste tab de nombres entiers et qui renvoie la liste triée par ordre croissant. Il est demandé de ne pas créer de nouvelle liste mais de modifier celle fournie.

On utilisera l’algorithme suivant :

  • on recherche le plus petit élément de la liste, en la parcourant du rang 0 au dernier rang, et on l'échange avec l'élément d'indice 0 ;
  • on recherche ensuite le plus petit élément de la liste restreinte du rang 1 au dernier rang, et on l'échange avec l'élément d'indice 1 ;
  • on continue de cette façon jusqu'à ce que la liste soit entièrement triée.

Exemple : 

>>> tri_selection([1, 52, 6, -9, 12])
[-9, 1, 6, 12, 52]


1
2
3
4
5
6
7
8
def tri_selection(tab):
    for i in range(len(tab)-1):
        indice_min = i
        for j in range(i+1, len(tab)):
            if tab[j] < tab[indice_min]:
                indice_min = j
        tab[i], tab[indice_min] = tab[indice_min], tab[i]
    return tab

➡ Rédigez votre code sur Basthon

Exercice 42.2

Le jeu du « plus ou moins » consiste à deviner un nombre entier choisi entre 1 et 99.

Un élève de NSI décide de le coder en langage Python de la manière suivante :

  • le programme génère un nombre entier aléatoire compris entre 1 et 99 ;
  • si la proposition de l’utilisateur est plus petite que le nombre cherché, l’utilisateur en est averti. Il peut alors en tester un autre ;
  • si la proposition de l’utilisateur est plus grande que le nombre cherché, l’utilisateur en est averti. Il peut alors en tester un autre ;
  • si l’utilisateur trouve le bon nombre en 10 essais ou moins, il gagne ;
  • si l’utilisateur a fait plus de 10 essais sans trouver le bon nombre, il perd.

La fonction randint est utilisée.
Si a et b sont des entiers tels que a <= b, randint(a,b) renvoie un nombre entier compris entre a et b.

Compléter le code ci-dessous et le tester :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
from random import randint

def plus_ou_moins():
    nb_mystere = randint(1,...)
    nb_test = int(input("Proposez un nombre entre 1 et 99 : "))
    compteur = ...

    while nb_mystere != ... and compteur < ... :
        compteur = compteur + ...
        if nb_mystere ... nb_test:
            nb_test = int(input("Trop petit ! Testez encore : "))
        else:
            nb_test = int(input("Trop grand ! Testez encore : "))

    if nb_mystere == nb_test:
        print ("Bravo ! Le nombre était ",...)
        print("Nombre d'essais: ",...)
    else:
        print ("Perdu ! Le nombre était ",...)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
from random import randint

def plus_ou_moins():
    nb_mystere = randint(1,99)
    nb_test = int(input('Proposez un nombre entre 1 et 99 : '))
    compteur = 1

    while nb_mystere != nb_test and compteur < 10 :
        compteur = compteur + 1
        if nb_mystere > nb_test:
            nb_test = int(input('Trop petit ! Testez encore : '))
        else:
            nb_test = int(input('Trop grand ! Testez encore : '))

    if nb_mystere == nb_test:
        print ('Bravo ! Le nombre était ', nb_mystere)
        print('Nombre d essais: ', compteur)
    else:
        print ('Perdu ! Le nombre était ', nb_mystere)

➡ Complétez le code sur Basthon

Exercice 43.1

Écrire une fonction ecriture_binaire_entier_positif qui prend en paramètre un entier positif n et renvoie une liste d'entiers correspondant à l‘écriture binaire de n.

Ne pas oublier d’ajouter au corps de la fonction une documentation et une ou plusieurs assertions pour vérifier les pré-conditions.

Exemples :

>>> ecriture_binaire_entier_positif(0)
[0]
>>> ecriture_binaire_entier_positif(2)
[1, 0]
>>> ecriture_binaire_entier_positif(105)
[1, 1, 0, 1, 0, 0, 1]

Aide :

  • l'opérateur // donne le quotient de la division euclidienne : 5//2 donne 2 ;
  • l'opérateur % donne le reste de la division euclidienne :5%2 donne 1 ;
  • append est une méthode qui ajoute un élément à une liste existante : Soit T=[5,2,4], alors T.append(10) ajoute 10 à la liste T. Ainsi, T devient [5,2,4,10].
  • reverse est une méthode qui renverse les éléments d'une liste. Soit T=[5,2,4,10]. Après T.reverse(), la liste devient [10,4,2,5].

On remarquera qu’on récupère la représentation binaire d’un entier n en partant de la gauche en appliquant successivement les instructions :

b = n%2

n = n//2

répétées autant que nécessaire.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
def ecriture_binaire_entier_positif(n):
    # cas particulier pour n = 0
    if n == 0:
        return [0]
    # cas général
    b = []
    while n != 0:
        b.append(n % 2)
        n = n // 2
    b.reverse()
    return b

➡ Rédigez votre code sur Basthon

Exercice 43.2

La fonction tri_bulles prend en paramètre une liste T d’entiers non triés et renvoie la liste triée par ordre croissant.

Le tri à bulles est un tri en place qui commence par placer le plus grand élément en dernière position en parcourant la liste de gauche à droite et en échangeant au passage les éléments voisins mal ordonnés (si la valeur de l’élément d’indice i a une valeur strictement supérieure à celle de l’indice i + 1, ils sont échangés). Le tri place ensuite en avant-dernière position le plus grand élément de la liste privée de son dernier élément en procédant encore à des échanges d’éléments voisins. Ce principe est répété jusqu’à placer le minimum en première position.

Exemple : pour trier la liste [7, 9, 4, 3] :

  • première étape : 7 et 9 ne sont pas échangés, puis 9 et 4 sont échangés, puis 9 et 3 sont échangés, la liste est alors [7, 4, 3, 9]
  • deuxième étape : 7 et 4 sont échangés, puis 7 et 3 sont échangés, la liste est alors [4, 3, 7, 9]
  • troisième étape : 4 et 3 sont échangés, la liste est alors [3, 4, 7, 9]

Compléter le code Python ci-dessous qui implémente la fonction tri_bulles.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def tri_bulles(T):
    '''
    Renvoie le tableau T trié par ordre croissant
    '''
    n = len(T)
    for i in range(...,...,-1):
        for j in range(i):
            if T[j] > T[...]:
                ... = T[j]
                T[j] = T[...]
                T[j+1] = temp
    return T

Exemples : 

>>> tri_bulles([])
[]
>>> tri_bulles([7])
[7]
>>> tri_bulles([9, 3, 7, 2, 3, 1, 6])
[1, 2, 3, 3, 6, 7, 9]
>>> tri_bulles([9, 7, 4, 3])
[3, 4, 7, 9]


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def tri_bulles(T):
    '''
    Renvoie le tableau T trié par ordre croissant
    '''
    n = len(T)
    for i in range(n-1,-1,-1):
        for j in range(i):
            if T[j] > T[j+1]:
                temp = T[j]
                T[j] = T[j+1]
                T[j+1] = temp
    return T

➡ Complétez le code sur Basthon

Exercice 44.1

Programmer une fonction renverse, prenant en paramètre une chaîne de caractères non vide mot et renvoie une chaîne de caractères en inversant ceux de la chaîne mot.

Exemple :

>>> renverse("informatique")
"euqitamrofni"

1
2
3
4
5
def renverse(mot):
    sol = ''
    for lettre in mot:
        sol = lettre + sol
    return sol

➡ Rédigez votre code sur Basthon

Exercice 44.2

Un nombre premier est un nombre entier naturel qui admet exactement deux diviseurs distincts entiers et positifs : 1 et lui-même.

Le crible d’Ératosthène permet de déterminer les nombres premiers plus petit qu’un certain nombre n fixé.

On considère pour cela un tableau tab de nbooléens, initialement tous égaux à True, sauf tab[0] et tab[1] qui valent False, 0 et 1 n’étant pas des nombres premiers.

On parcourt alors ce tableau de gauche à droite.

Pour chaque indice i :

  • si tab[i] vaut True : le nombre i est premier et on donne la valeur False à toutes les cases du tableau dont l’indice est un multiple de i, à partir de 2*i (c’est-à-dire 2*i, 3*i ...).

  • si tab[i] vaut False : le nombre i n’est pas premier et on n’effectue aucun changement sur le tableau.

On dispose de la fonction crible, incomplète et donnée ci-dessous, prenant en paramètre un entier n strictement positif et renvoyant un tableau contenant tous les nombres premiers plus petits que n.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
def crible(n):
    """
    Renvoie un tableau contenant tous les nombres premiers plus petits que N
    """
    premiers = []
    tab = [True] * n
    tab[0], tab[1] = False, False
    for i in range(..., n):
        if tab[i] == ...:
            premiers.append(...)
            for multiple in range(2*i, n, ...):
                tab[multiple] = ...
    return premiers

assert crible(40) == [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37]

Compléter le code de cette fonction.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
def crible(n):
    """
    Renvoie un tableau contenant tous les nombres premiers plus petits que N
    """
    premiers = []
    tab = [True] * n
    tab[0], tab[1] = False, False
    for i in range(2, n):
        if tab[i] == True:
            premiers.append(i)
            for multiple in range(2*i, n, i):
                tab[multiple] = False
    return premiers

assert crible(40) == [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37]

➡ Complétez le code sur Basthon

Exercice 45.1

On veut trier par ordre croissant les notes d’une évaluation qui sont des nombres entiers compris entre 0 et 10 (inclus).

Ces notes sont contenues dans une liste notes_eval.

Écrire une fonction rangement_valeurs prenant en paramètre la liste notes_eval et renvoyant une liste de longueur 11 telle que la valeur de cette liste à chaque rang est égale au nombre de notes valant ce rang. Ainsi le terme de rang 0 indique le nombre de note 0, le terme de rang 1 le nombre de note 1, etc.

Écrire ensuite une fonction notes_triees prenant en paramètre la liste des effectifs des notes et renvoyant une liste contenant la liste, triée dans l’ordre croissant, des notes des élèves.

Exemple :

>>> notes_eval = [2, 0, 5, 9, 6, 9, 10, 5, 7, 9, 9, 5, 0, 9, 6, 5, 4]

>>> effectifs_notes = rangement_valeurs(notes_eval)
>>> effectifs_notes
[2, 0, 1, 0, 1, 4, 2, 1, 0, 5, 1]

>>> notes_triees(effectifs_notes)
[0, 0, 2, 4, 5, 5, 5, 5, 6, 6, 7, 9, 9, 9, 9, 9, 10]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
def rangement_valeurs(notes_eval):
    lst = [0]*11
    for note in notes_eval:
        lst[note] += 1
    return lst

def notes_triees(effectifs_notes):
    triees = []
    for i in range(11):
        if effectifs_notes[i] != 0:
            for _ in range(effectifs_notes[i]):
                triees.append(i)
    return triees

➡ Rédigez votre code sur Basthon

Exercice 45.2

L’objectif de cet exercice est d’écrire deux fonctions récursives dec_to_bin et bin_to_dec assurant respectivement la conversion de l’écriture décimale d’un nombre entier vers son écriture en binaire et, réciproquement, la conversion de l’écriture en binaire d’un nombre vers son écriture décimale.

Dans cet exercice, on s’interdit l’usage des fonctions Python bin et int.

On rappelle sur l’exemple ci-dessous une façon d’obtenir l’écriture en binaire du nombre 25 :

\(25 = 1 + 2 \times 12\)
\(\phantom{25} = 1 + 2 \times 12\)
\(\phantom{25} = 1 + 2 (0 + 2 \times 6)\)
\(\phantom{25} = 1 + 2 (0 + 2 (0 + 2 \times 3))\)
\(\phantom{25} = 1 + 2 (0 + 2 (0 + 2 (1 + 2 \times 1)))\)
\(\phantom{25} = 1 \times 2^0 + 0 \times 2^1 + 0 \times 2^2 + 1 \times 2^3 + 1 \times 2^4\)




L'écriture binaire de 25 est donc 11001.

0n rappelle également que :

  • a // 2 renvoie le quotient de la division euclidienne de a par 2.
  • a % 2 renvoie le reste dans la division euclidienne de a par 2.

On indique enfin qu’en Python si mot = "informatique" alors :

  • mot[-1] renvoie 'e', c’est-à-dire le dernier caractère de la chaîne de caractères mot.
  • mot[:-1] renvoie 'informatiqu' , c’est-à-dire l’ensemble de la chaîne de caractères mot privée de son dernier caractère.

Compléter, puis tester, les codes de deux fonctions ci-dessous. On précise que la fonction récursive dec_to_bin prend en paramètre un nombre entier et renvoie une chaîne de caractères contenant l’écriture en binaire du nombre passé en paramètre.

Exemple :

>>> dec_to_bin(25)
'11001'

La fonction récursive bin_to_dec prend en paramètre une chaîne de caractères représentant l’écriture d’un nombre en binaire et renvoie l’écriture décimale de ce nombre.

>>> bin_to_dec('101010')
42

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
def dec_to_bin(nb_dec):
    q, r = nb_dec // 2, nb_dec % 2
    if q == ...:
        return str(r)
    else:
        return dec_to_bin(...) + ...

def bin_to_dec(nb_bin):
    if nb_bin == '0':
        return 0
    elif ...:
        return 1
    else:
        if nb_bin[-1] == '0':
            bit_droit = 0
        else:
            bit_droit = ...
        return ... * bin_to_dec(nb_bin[:-1]) + ...

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
def dec_to_bin(nb_dec):
    q, r = nb_dec // 2, nb_dec % 2
    if q == 0:
        return str(r)
    else:
        return dec_to_bin(q) + str(r)

def bin_to_dec(nb_bin):
    if nb_bin == '0':
        return 0
    elif nb_bin == '1':
        return 1
    else:
        if nb_bin[-1] == '0':
            bit_droit = 0
        else:
            bit_droit = 1
        return 2 * bin_to_dec(nb_bin[:-1]) + bit_droit

➡ Complétez le code sur Basthon

Sujets et corrigés : autres ressources

Un site centralise sujets et corrigés : c'est ici

Les sujets Term sont également corrigés en ligne ici