Algorithmique Premiere

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°197
La fonction suivante doit calculer la moyenne d'un tableau de nombres, passé en paramètre. Avec quelles expressions faut-il compléter l'écriture pour que la fonction soit correcte ? :

def moyenne(tableau) :  
     total = ...  
     for valeur in tableau :  
          total = total + valeur  
     return total / .....  

• 0 et len(tableau)
• 0 et len(tableau) + 1
• 1 et len(tableau)
• 1 et len(tableau) + 1

Algorithmique (Première) - Tri par insertion/sélection

n°198
Quelle valeur retourne la fonction 'mystere' suivante ?

def mystere(liste):  
     valeur_de_retour = True  
     indice = 0  
     while indice < len(liste) - 1 :  
          if liste[indice] > liste[indice + 1]:  
               valeur_de_retour = False  
          indice = indice + 1  
     return valeur_de_retour  

• Une valeur booléenne indiquant si la liste liste passée en paramètre est triée
• La valeur du plus grand élément de la liste passée en paramètre
• La valeur du plus petit élément de la liste passée en paramètre.
• Une valeur booléenne indiquant si la liste passée en paramètre contient plusieurs fois le même élément

Algorithmique (Première) - Algorithme KNN

n°199
A quelle catégorie appartient l'algorithme des k plus proches voisins ?

• Algorithmes de classification et d'apprentissage
• Algorithmes de recherche de chemins
• Algorithmes de tri
• Algorithmes gloutons

Algorithmique (Première) - Tri par insertion/sélection

n°200
Combien d'échanges effectue la fonction Python suivante pour trier un tableau de 10 éléments au pire des cas ?

def tri(tab) :  
     for i in range (1, len(tab)) :  
          for j in range (len(tab) - i) :  
               if tab[j] > tab[j+1] :  
                    tab[j], tab[j+1] = tab[j+1], tab[j]  

• 45
• 100
• 10
• 55

Algorithmique (Première) - Recherche Dichotomique

n°201
Avec un algorithme de recherche par dichotomie, combien d'étapes sont nécessaires pour déterminer que 35 est présent dans le tableau [1, 7, 12, 16, 18, 20, 24, 28, 35, 43, 69] ?

• 2 étapes
• 1 étape
• 9 étapes
• 11 étapes

Algorithmique (Première) - Recherche Dichotomique

n°202
Pour pouvoir utiliser un algorithme de recherche par dichotomie dans une liste, quelle précondition doit être vraie ?

• La liste doit être triée
• La liste ne doit pas comporter de doublons
• La liste doit comporter uniquement des entiers positifs
• La liste doit être de longueur inférieure à 1024

Algorithmique (Première) - Autres

n°203
A désignant un entier, lequel des codes suivants ne termine pas ?

• i = A + 1
  while i < A :
       i = i - 1
  

• i = A + 1
  while i < A :
       i = i + 1
  

• i = A - 1
  while i < A :
       i = i - 1
  

• i = A - 1
  while i < A :
       i = i + 1
  

Algorithmique (Première) - Tri par insertion/sélection

n°204
On considère la fonction suivante :

def f(t,i) :  
     im = i  
     m = t[i]  
     for k in range(i+1, len(t)) :  
          if t[k] < m :  
               im, m = k, t[k]  
     return im  

Que vaut l'expression f([7, 3, 1, 8, 19, 9, 3, 5], 0) ?

• 1
• 2
• 3
• 4

Algorithmique (Première) - Algorithme KNN

n°214
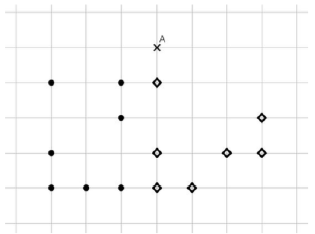
Dans le quadrillage ci-dessous 14 points sont dessinés, dont 7 de la classe C1, avec des ronds noirs •,et 7 de la classe C2, avec des losanges ◇. On introduit un nouveau point A, dont on cherche la classe à l'aide d'un algorithme des k plus proches voisins pour la distance géométrique habituelle, en faisant varier la valeur de k parmi 1, 3 et 5. Quelle est la bonne réponse (sous la forme d'un triplet de classes pour le triplet (1,3,5) des valeurs de k) ?

• C1, C2, C3
• C2, C1, C2
• C2, C2, C2
• C2, C1, C1

Algorithmique (Première) - Autres

n°247
Parmi les affirmations suivantes, laquelle est vraie ?

• Deux algorithmes de coûts identiques effectuent exactement le même nombre d'opérations.
• Le coût d'un algorithme permet d'évaluer un temps d'exécution.
• Plus le coût d'un algorithme est élevé, plus précis est le résultat.
• Une recherche dichotomique a un coût deux fois plus élevé que celui d'une recherche linéaire puisque 'dichotomie' signifie 'division en deux parties'

Algorithmique (Première) - Autres

n°248
On considère le code qui suit où la valeur de n est un entier naturel :

x = 1  
while x < n :  
     x = 2 * x  

On s'intéresse au coût de cet algorithme en fonction de n. Parmi les affirmations suivantes, laquelle est vraie ?

• Le coût est semblable à celui d'une recherche dichotomique.
• Le coût est linéaire en fonction de n.
• Le coût est quadratique en fonction de n.
• Il est impossible de connaître le coût.

Algorithmique (Première) - Autres

n°249
Dans la fonction suivante, les valeurs des variables x et y sont des entiers naturels :

def f(x, y) :  
    s = x  
    t = y  
    while t > 0 :  
        s = s + 1  
        t = t - 1  
    return s  

Quelle affirmation est fausse ?

• La propriété 's + t = x + y' est un invariant de boucle.
• La valeur finale de t est 1
• La propriété 't est supérieur ou égal à 0' est un invariant de la boucle while.
• Le résultat renvoyé est égal à la somme a + b.

Algorithmique (Première) - Autres

n°250
On écrit un programme pour chercher le mot 'an' dans une chaîne de caractères (cette chaîne contient au moins deux caractères). Pour cela on parcourt la chaîne et si on trouve un 'a', on vérifie si le caractère suivant est un 'n'. Si oui, le programme s'arrête. Il faut faire attention au dépassement d'indice qui provoquerait une erreur. Quelle affirmation est vraie ?

• La recherche de 'a' a un coût linéaire et le coût de l'algorithme est deux fois plus élevé donc il n'est pas linéaire.
• Dans le pire des cas, le nombre de comparaisons est exactement 2n.
• Dans le pire des cas, le nombre de comparaisons est exactement 2n-1.
• Dans le pire des cas, le nombre de comparaisons est exactement 2n-2.

Algorithmique (Première) - Recherche Dichotomique

n°251
Un algorithme de recherche dichotomique dans une liste triée de taille n nécessite exactement k comparaisons dans le pire des cas. Combien de comparaisons sont nécessaires avec le même algorithme pour une liste de taille 2n ?

• 2k + 1 comparaisons.
• 2k comparaisons.
• k + 2 comparaisons.
• k + 1 comparaisons.

Algorithmique (Première) - Tri par insertion/sélection

n°252
Un algorithme cherche la valeur maximale d'une liste non triée de taille n. Combien de temps mettra cet algorithme sur une liste de taille 2n ?

• Le même temps que sur la liste de taille n si le maximum est dans la première moitié de la liste.
• On a ajouté n valeurs, l'algorithme mettra donc n fois plus de temps que sur la liste de taille n.
• Le temps sera simplement doublé par rapport au temps mis sur la liste de taille n.
• On ne peut pas savoir, tout dépend de l'endroit où est le maximum.

Algorithmique (Première) - Tri par insertion/sélection

n°253
Quel est le coût en temps dans le pire des cas du tri par insertion ?

• O(n)
• O(n2)
• O(2n)
• O(log(n))

Algorithmique (Première) - Algorithme KNN

n°254
Soit les points de coordonnées suivantes :

A(1, 6)  
B(2, 6)  
C(3, 1)  
D(4, 2)  
E(6, 0)  
F(7, 5)  
G(7, 3)  
H(10, 3)  

En utilisant la distance euclidienne, quels sont les deux plus proches voisins du point P(5,5) ?

• les points A et B.
• les points D et E.
• les points F et G.
• les points B et F.

Algorithmique (Première) - Algorithmes Gloutons

n°255
Un système monétaire contient les pièces suivantes : 20, 15, 7, 4 et 2 unités. Le nombre de pièces de chaque sorte n'est pas limité. On souhaite rendre 38 unités. Quelle est la solution donnée par l'algorithme glouton de rendu de monnaie ?

• [15, 15, 4, 4]
• [20, 7, 7, 4]
• [7, 7, 7, 7, 4, 4, 2]
• L'algorithme échouera à rendre la somme de 38 unités.

Algorithmique (Première) - Algorithmes Gloutons

n°256
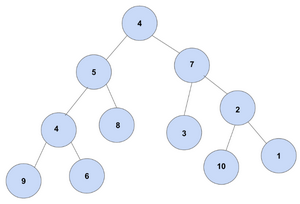
Voici un arbre, on le parcourt en partant du haut (la racine) et en descendant de branche en branche (les noeuds) jusqu'à arriver à une feuille.
Par exemple on peut faire le parcourt Racine 4 puis noeud 5 puis noeud 4 puis feuille 6.
Considérons un algorithme Glouton de parcours (racine vers feuille) de cet arbre, Sélectionnant le noeud le plus grand à chaque étape.
Quel chemin cet algorithme Glouton va-t-il parcourir ?

• 4-->7-->3
• 4-->5-->8
• 9-->10-->8).
• 4-->5-->4-->9

Algorithmique (Première) - Algorithmes Gloutons

n°257
On considère le problème où l’on doit rendre 8 euros de monnaie.
On dispose de pièces de 1,4,6 euros.
Indiquer le rendu de monnaie donné par un algorithme glouton.

• 4;4
• 6;1;1
• 4;1;1;1;1
• 1;1;1;1;1;1;1;1

Algorithmique (Première) - Recherche Dichotomique

n°267
On souhaite écrire une fonction recherche_dichotomique(t, v), qui renvoie une position v dans le tableau t, supposé trié, et None si v ne s'y trouve pas : parmi les 4 fonctions ci-dessous, laquelle est correcte ?

• def recherche_dichotomique (t, v) :  
       g = 0  
       d = len(t) - 1  
       while g <= d :  
            m = (g + d) // 2  
            if t[m] < v :  
                 g = m + 1  
            elif t[m] > v :  
                 d = m - 1  
            else :  
                 return m  
       return None  
  

• def recherche_dichotomique (t, v) :  
       g = 0  
       d = len(t) - 1  
       while g <= d :  
            m = (g + d) // 2  
            if t[m] > v :  
                 g = m + 1  
            elif t[m] < v :  
                 d = m - 1  
            else :  
                 return m  
       return None  
  

• def recherche_dichotomique (t, v) :  
       g = 0  
       d = len(t)  
       while g <= d :  
            m = (g + d) // 2  
            if t[m] < v :  
                 g = m + 1  
            elif t[m] > v :  
                 d = m - 1  
            else :  
                 return m  
       return None  
  

• def recherche_dichotomique (t, v) :  
       g = 0  
       d = len(t) - 1  
       while g < d :  
            m = (g + d) // 2  
            if t[m] < v :  
                 g = m + 1  
            elif t[m] > v :  
                 d = m - 1  
            else :  
                 return m  
       return None  
  

Algorithmique (Première) - Tri par insertion/sélection

n°270
On souhaite écrire une fonction tri_selection(t), qui trie le tableau t dans l'ordre croissant : parmi les 4 programmes suivants, lequel est correct ?

• def tri_selection(t) :  
       for i in range (len(t)-1) :  
            min = i          
            for j in range(i+1,len(t)):  
                 if t[j] < t[min]:  
                      min = j  
            tmp = t[i]  
            t[i] = t[min]  
            t[min] = tmp  
  

• def tri_selection(t) :  
       for i in range (len(t)-1) :  
            min = i          
            for j in range(i+1,len(t)-1):  
                 if t[j] < t[min]:  
                      min = j  
            tmp = t[i]  
            t[i] = t[min]  
            t[min] = tmp  
  

• def tri_selection(t) :  
       for i in range (len(t)-1) :  
            min = i          
            for j in range(i+1,len(t)):  
                 if t[j] < min:  
                      min = j  
            tmp = t[i]  
            t[i] = t[min]  
            t[min] = tmp  
  

• def tri_selection(t) :  
       for i in range (len(t)-1) :  
            min = i          
            for j in range(i+1,len(t)):  
                 if t[j] < t[min]:  
                      min = j  
            tmp = t[i]  
            t[min] = t[i]  
            t[i] = tmp  
  

Algorithmique (Première) - Algorithmes Gloutons

n°271
Rendu de monnaie :
euros = [0, 1, 2, 5, 10, 20, 50, 100]
On souhaite écrire un programme qui affiche la monnaie que le commerçant devra rendre. Parmi les 4 programmes suivants, lequel est correct ?

• def monnaie(s) :              
       i = len(euros) - 1                  
       p = 0                               
       while s > 0 :  
            if s >= euros[i] :              
                 p +=1         
                 s -= euros[i]           
            else :  
                 i = i - 1  
       return p  
  

• def monnaie(s) :              
       i = len(euros)                  
       p = 0                               
       while s > 0 :  
            if s >= euros[i] :              
                 p +=1         
                 s -= euros[i]           
            else :  
                 i = i - 1  
       return p  
  

• def monnaie(s) :              
       i = len(euros) - 1                  
       p = 0                               
       while s >= 0 :  
            if s >= euros[i] :              
                 p +=1         
                 s -= euros[i]           
            else :  
                 i = i - 1  
       return p  
  

• def monnaie(s) :              
       i = len(euros) - 1                  
       p = 0                               
       while s > 0 :  
            if s > euros[i] :              
                 p +=1         
                 s -= euros[i]           
            else :  
                 i = i - 1  
       return p  
  

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°281
On considère le programme ci-dessous. Quel est le résultat de mystere([2,1,1,4,1,5,2,4], [3,2,1,4,5]) ?

def mystere(liste1, liste2):  
    res = 0  
    for e1 in liste1:  
        for e2 in liste2:  
            if e1 == e2:  
                res += 1  
    return res  

• 0
• 4
• 8
• 40

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°282
Soit la fonction ci-dessous :

def foo(lst1,lst2):  
    lst=[(random.choice(lst1),random.choice(lst2))]  
    n = 1  
    while n <= 2:  
        a = random.choice(lst1)  
        b = random.choice(lst2)  
        if (a,b) not in lst:  
            lst.append((a,b))  
            n = n + 1  
    return lst  

On rappelle que random.choice(liste) renvoie un élément choisi aléatoirement dans liste.
Parmi les propositions suivantes laquelle est valide ?

• foo([1,2,3],['A','B','C']) peut valoir [(3, 'C'), (3, 'A'), (1, 'A')]
• foo([1,2,3],['A','B','C']) peut valoir [(1, 'C'), (3, 'A'), (1, 'C')]
• foo([1,2,3],['A','B','C']) peut valoir [(3, 'C'), (3, 'A')]
• foo([1,2,3],['A','B','C']) peut valoir [(1, 'C'), (3, 'C')]

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°303
On considère la fonction suivante.

def mystere(tab):  
    booleen = True  
    for i in range(len(tab)-1):  
        if tab[i] > tab[i+1]:  
            booleen = False  
    return booleen  

Que renvoie l'appel mystere([1, 2, 7, 3, 10]) ?

• False
• True
• [1, 2, 3, 7, 10]
• On ne peut pas savoir

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°307
On considère la fonction suivante.

def mystere(v, T):  
    ''' T est un tableau d'entiers et v est un entier'''  
    n = 0  
    for e in T:  
        if e == v:  
            n = n + 1  
    return n  

Que renvoie l'expression mystere(1, [1, 2, 1, 3, 4, 6, 7, 2, 1, 2]) ?

• 3
• 2
• 10
• 1

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°308
On considère la fonction suivante.

def hamming(t1, t2):  
    ''' t1 et t2 sont deux tableaux de même taille, constitués d'entiers'''  
    d = 0  
    for i in range(len(t1)):  
        if t1[i] != t2[i]:  
            d = d + 1  
    return d  

Que renvoie l'appel hamming([1, 2, 3, 4, 5], [1, 3, 2, 4, 5]) ?

• True
• False
• 3
• 2

Algorithmique (Première) - Tri par insertion/sélection

n°318
Soit le programme de tri suivant :

def tri(lst):  
    for i in range(1,len(lst)):  
        valeur = lst[i]  
        j = i  
        while j>0 and lst[j-1]>valeur:  
            lst[j]=lst[j-1]  
            j = j-1  
        lst[j]=valeur_a_inserer  

De quel type de tri s'agit-il ?

• Tri par insertion
• Tri fusion
• Tri par sélection
• Tri à bulles

Algorithmique (Première) - Tri par insertion/sélection

n°319
Soit le programme de tri suivant :

def tri(lst):  
    nb = len(lst)  
    for i in range(0,nb):      
        ind_plus_petit = i  
        for j in range(i+1,nb) :  
            if lst[j] < lst[ind_plus_petit] :  
                ind_plus_petit = j  
        if ind_plus_petit is not i :  
            temp = lst[i]  
            lst[i] = lst[ind_plus_petit]  
            lst[ind_plus_petit] = temp  

De quel type de tri s'agit-il ?

• Tri par insertion
• Tri fusion
• tri par selection
• tri à bulles

Algorithmique (Première) - Autres

n°400
On a saisi le code suivant :

tab = [10, 8, 4, 3, 1, 5, 7, 2]  
cpt = 0  
for i in range(1, len(tab)):  
    for j in range(len(tab) - i):  
        cpt +=1  

Que contient la variable cpt à la fin de l’exécution de ce script ?

• 64
• 8
• 36
• 28

Algorithmique (Première) - Autres

n°403
On a saisi le code suivant :

def mystere(texte):  
    status = False  
    for i in range(len(texte)-1):  
        if (texte[i] == texte[i+1]):  
            status = True  
    return status  

Dans quel cas la fonction mystere renvoie le booléen False ?

• mystere('alphabet')
• mystere('voyelle')
• mystere('dictionnaire')
• mystere('lettre')

Algorithmique (Première) - Autres

n°404
On a saisi le code suivant :

def mystere(texte,n):  
    chaine = ''  
    for i in range(len(texte)):  
        if (i % 2 == 0):   
            chaine = chaine + texte[i]*n  
    return chaine  

Que retourne l'instruction mystere('chocolat',4) ?

• 'cccchhhhoooollllaaaatttt'
• 'chocolatchocolatchocolatchocolat'
• 'ccccooooooooaaaa'
• 'hhhhcccclllltttt'

Algorithmique (Première) - Autres

n°496
L'algorithme suivant permet de calculer la somme des N premiers entiers, où N est un nombre entier donné :

i =0  
somme =0  
while i < N :  
    i = i +1  
    somme = somme + i  

Un invariant de boucle de cet algorithme est le suivant :

• somme = 0 + 1 + 2 + ... + i et i < N
• somme = 0 + 1 + 2 + ... + N et i < N
• somme = 0 + 1 + 2 + ... + i et i < N+1
• somme = 0 + 1 + 2 + ... + N et i < N+1

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°497
Quelle est la valeur de c à la fin de l'exécution du code suivant :

L = [1,2,3,4,1,2,3,4,0,2]  
c = 0  
for k in L:  
    if k == L[1]:  
        c = c+1  

• 0
• 2
• 3
• 10

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°498
On considère la fonction Python suivante, qui prend en argument une liste L et renvoie le maximum des éléments de la liste :

def rechercheMaximum(L):  
    max = L[0]  
    for i in range(len(L)):  
       if L[i] > max:  
           max = L[i]  
    return max  

On note n la taille de la liste.
Quelle est la complexité en nombre d’opérations de l’algorithme ?

• constante, c’est-à-dire ne dépend pas de n
• linéaire, c’est-à-dire de l’ordre de n
• quadratique, c’est-à-dire de l’ordre de n²
• cubique, c’est-à-dire de l’ordre de n3

Algorithmique (Première) - Autres

n°499
Quelle est la valeur du couple (s,i) à la fin de l'exécution du script suivant ?

s = 0  
i = 1  
while i < 5:  
    s = s + i  
    i = i + 1  

• (4, 5)
• (10, 4)
• (10, 5)
• (15, 5)

Algorithmique (Première) - Autres

n°500
Pour trier par sélection une liste de 2500 entiers, le nombre de comparaisons nécessaires à l’algorithme est de l’ordre de :

• 2500
• 2500
• 25002
• 22500

Algorithmique (Première) - Autres

n°501
En utilisant une recherche dichotomique, combien faut-il de comparaisons pour trouver une valeur dans un tableau trié de 1000 nombres ?

• 3
• 10
• 1000
• 1024

Algorithmique (Première) - Autres

n°613
On considère la fonction suivante :

def f(T,i):  
    indice = i  
    m = T[i]  
    for k in range(i+1, len(T)):  
        if T[k] < m:  
            indice = k  
            m = T[k]  
    return indice  

Quelle est la valeur de f([ 7, 3, 1, 8, 19, 9, 3, 5 ], 0) ?

• 1
• 2
• 3
• 4

Algorithmique (Première) - Autres

n°614
On considère la fonction suivante :

def comptage(phrase,lettre):  
          i = 0  
          for j in phrase:  
              if j == lettre:  
                  i = i+1  
          return i  

Que renvoie l'appel comptage('Vive l’informatique','e') ?

• 0
• 2
• 19
• 'e'

Algorithmique (Première) - Autres

n°615
Quelle est la valeur de element à la fin de l'exécution du code suivant :

L = [1,2,3,4,1,2,3,4,0,2]  
element = L[0]  
for k in L:  
    if k > element:  
        element = k  

• 0
• 1
• 4
• 10

Algorithmique (Première) - Autres

n°616
À quelle catégorie appartient l’algorithme classique de rendu de monnaie ?

• les algorithmes de classification et d'apprentissage
• les algorithmes de tri
• les algorithmes gloutons
• les algorithmes de mariages stables

Algorithmique (Première) - Autres

n°617
L'algorithme suivant permet de calculer la somme des N premiers entiers, où N est un nombre entier donné :

i =0  
somme =0  
while i < N :  
    i = i + 1  
    somme = somme + i  

Un invariant de boucle de cet algorithme est le suivant :

• somme = 0 + 1 + 2 + ... + i et i < N
• somme = 0 + 1 + 2 + ... + N et i < N
• somme = 0 + 1 + 2 + ... + i et i < N+1
• somme = 0 + 1 + 2 + ... + N et i < N+1

Algorithmique (Première) - Autres

n°618
Quelle est la valeur du couple (s,i) à la fin de l'exécution du script suivant ?

s = 0
i = 1
while i < 5:
    s = s + i
    i = i + 1

• (4, 5)
• (10, 4)
• (10, 5)
• (15, 5)

Algorithmique (Première) - Autres

n°655
Quelle est la complexité du tri par sélection ?

• inconnue
• linéaire
• quadratique
• exponentielle

Algorithmique (Première) - Autres

n°656
Soit L une liste de \(n\) nombres réels (\(n\) entier naturel non nul). On considère l'algorithme suivant, en langage Python, calculant la moyenne des éléments de L.

M = 0  
for k in range(n):  
    M = M + L[k]  
M = M/n

Si le nombre \(n\) de données double alors le temps d'exécution de ce script :

• reste le même
• double aussi
• est multiplié par \(n\)
• est multiplié par 4

Algorithmique (Première) - Autres

n°657
La fonction ci-dessous compte le nombre d'occurrences d'un élément x dans une liste L :

def compteur(L,x):  
    n = 0  
    for item in L:  
        if item == x:  
            n = n + 1  
    return n

Comment évolue le temps d'exécution d'un appel de cette fonction si on prend comme argument une liste deux fois plus grande ?

• c'est le même temps d'exécution
• le temps d'exécution est à peu près doublé
• le temps d'exécution est à peu près quadruplé
• impossible de le prévoir, cela dépend aussi de l'argument x

Algorithmique (Première) - Autres

n°658
La fonction mystere suivante prend en argument un tableau d'entiers.

def mystere(t):  
    for i in range(len(t) - 1):  
        if t[i+1] != t[i] + 1:  
            return False  
    return True

À quelle condition la valeur renvoyée par la fonction est-elle True ?

• si le tableau passé en argument est une suite d'entiers consécutifs
• si le tableau passé en argument est trié en ordre croissant
• si le tableau passé en argument est trié en ordre décroissant
• si le tableau passé en argument contient des entiers tous identiques

Algorithmique (Première) - Autres

n°659
Un algorithme de recherche dichotomique dans une liste triée de taille \(n\) nécessite, dans le pire des cas, exactement \(k\) comparaisons.
Combien cet algorithme va-t-il utiliser, dans le pire des cas, de comparaisons sur une liste de taille \(2n\) ?

• \(k\)
• \(k + 1\)
• \(2k\)
• \(2k + 1\)

Algorithmique (Première) - Autres

n°660
La fonction suivante doit déterminer la valeur maximale d'un tableau de nombres passé en argument. Avec quelles expressions faut-il remplacer les pointillés du script suivant pour que la fonction soit correcte ?

def maximum(T):  
    maxi = T[0]  
    n = len(T)  
    for i in range(i, .….):  
        if T[i] > maxi:  
            maxi = ......  
    return maxi

• n puis T[i]
• n puis T[i-1]
• n-1 puis T[i]
• n-1 puis T[i-1]

Algorithmique (Première) - Autres

n°697
\(a\) et \(m\) étant deux entiers supérieurs à 1, la fonction suivante renvoie \(a^{m}\).

def puissance(a,m):  
    p = 1  
    n = 0  
    while n < m:  
        #  
        p = p * a  
        n = n + 1  
    return p

Quelle est l'égalité qui est vérifiée à chaque passage par la ligne marquée # ?

• \(p = a^{n - 1}\)
• \(p = a^{n}\)
• \(p = a^{n + 1}\)
• \(p = a^{m}\)

Algorithmique (Première) - Autres

n°698
Quelle est la valeur de element à la fin de l'exécution du code suivant :

L = [1, 2, 3, 4, 1, 2, 3, 4, 0, 2]  
element = L[0]  
for k in L:  
    if k > element:  
        element = k

• 0
• 1
• 4
• 10

Algorithmique (Première) - Autres

n°699
On dispose en quantité illimité de pièces de 1 euro, 2 euros et 5 euros. On veut totaliser une somme de 18 euros. Quelle est la solution donnée par l’algorithme glouton ?

• [5, 5, 5, 2, 1]
• [5, 5, 5, 2, 2, 1]
• [5, 5, 2, 2, 2, 1, 1]
• [5, 2, 2, 2, 2, 1, 1, 1, 1, 1]

Algorithmique (Première) - Autres

n°700
On considère la fonction suivante :

def f(x,L):  
    g = 0  
    d = len(L)-1  
    while g < d:  
        m = (g+d)//2  
        if x <= L[m]:  
            d = m  
        else:  
            g = m + 1  
    return g

Cette fonction implémente :

• le tri par insertion
• le tri par sélection
• la recherche dichotomique
• la recherche du plus proche voisin

Algorithmique (Première) - Autres

n°701
On considère la fonction suivante :

def comptage(phrase,lettre):  
    i = 0  
    for j in phrase:  
        if j == lettre:  
            i = i+1  
    return i  

Que renvoie l'appel comptage('Vive l’informatique','e') ?

• 0
• 2
• 19
• 'e'

Algorithmique (Première) - Autres

n°702
Quelle est la valeur du couple (s,i) à la fin de l'exécution du script suivant ?

s = 0
i = 1
while i < 5:
    s = s + i
    i = i + 1

• (4, 5)
• (10, 4)
• (10, 5)
• (15, 5)

Algorithmique (Première) - Autres

n°739
À la fin de l'exécution du code suivant, quelle sera la valeur de la variable cpt ?

a = 1  
cpt = 20  
while cpt > 8:  
    a = 2*a  
    cpt = cpt - 1  

• 0
• 7
• 8
• 9

Algorithmique (Première) - Autres

n°740
En utilisant une recherche dichotomique, combien faut-il de comparaisons pour trouver une valeur dans un tableau trié de 1000 nombres ?

• 3
• 10
• 1000
• 1024

Algorithmique (Première) - Autres

n°741
Un algorithme de recherche dichotomique dans une liste triée de taille \(n\) nécessite, dans le pire des cas, exactement \(k\) comparaisons.
Combien cet algorithme va-t-il utiliser, dans le pire des cas, de comparaisons sur une liste de taille \(2n\) ?

• \(k\)
• \(k + 1\)
• \(2k\)
• \(2k + 1\)

Algorithmique (Première) - Autres

n°742
On définit la fonction suivante :

def traitement(liste) :  
    m = liste[0]  
    for i in range (len(liste)) :  
        if liste[i] > m:  
            m = liste[i]  
    return m  

Que vaut traitement([-2,5,6,-10,35]) ?

• None
• -10
• -6
• 35

Algorithmique (Première) - Autres

n°743
\(a\) et \(m\) étant deux entiers supérieurs à 1, la fonction suivante renvoie \(a^{m}\).

def puissance(a,m):  
    p = 1  
    n = 0  
    while n < m:  
        p = p * a  
        #  
        n = n + 1  
    return p  

Quelle est l'égalité qui est vérifiée à chaque passage par la ligne marquée # ?

• \(p = a^{n - 1}\)
• \(p = a^{n}\)
• \(p = a^{n + 1}\)
• \(p = a^{m}\)

Algorithmique (Première) - Autres

n°744
Quelle valeur permet de compléter l’affirmation suivante : « Le nombre d’opérations nécessaires pour rechercher un élément séquentiellement dans un tableau de longueur \(n\) est de l’ordre de … » ?

• 1
• \(n\)
• \(n^{2}\)
• \(n^{3}\)

Algorithmique (Première) - Autres

n°823
Que fait la fonction suivante :

def trouver(L):
    i = 0
    for j in range(1, len(L))
        if L[j] >= L[i]:
            i = j
    return i

• elle renvoie le maximum de la liste
• elle renvoie le minimum de la liste
• elle renvoie l’indice de la première occurrence du maximum de la liste
• elle renvoie l’indice de la dernière occurrence du maximum de la liste

Algorithmique (Première) - Autres

n°825
Quel est le coût d'un algorithme de tri par insertion ?

• constant
• logarithmique
• linéaire
• quadratique

Algorithmique (Première) - Autres

n°826
Combien d’échanges effectue la fonction Python suivante pour trier un tableau de 10 éléments au pire des cas ?

def tri(tab):
    for i in range(1, len(tab)):
        for j in range(len(tab) - i):
            if tab[j]>tab[j+1]:
                tab[j],tab[j+1] = tab[j+1], tab[j]

• 10
• 45
• 55
• 100

Algorithmique (Première) - Autres

n°827
On exécute le code suivant :

tab = [1, 4, 3, 8, 2]
S = 0
for i in range(len(tab)):
    S = S + tab[i]

Que vaut la variable S à la fin de l'exécution ?

• 1
• 8
• 18
• 3.6

Algorithmique (Première) - Autres

n°828
On dispose de sacs de jetons portant les nombres 10, 5, 3 et 1.
On veut obtenir un total de 21 en utilisant ces jetons.
Si on utilise le principe de l'algorithme glouton, quelle addition va-t-on réaliser pour obtenir ce total de 21 ?

• 5 + 5 + 5 + 5 + 1
• 10 + 5 + 3 + 3
• 10 + 5 + 5 + 1
• 10 + 10 + 1

Algorithmique (Première) - Autres

n°865
La fonction mystere suivante prend en argument un tableau d'entiers.

def mystere(t):  
    for i in range(len(t) - 1):  
        if t[i] + 1 != t[i+1]:  
            return False  
    return True  

À quelle condition la valeur renvoyée par la fonction est-elle True ?

• si le tableau passé en argument est une suite d'entiers consécutifs
• si le tableau passé en argument est trié en ordre croissant
• si le tableau passé en argument est trié en ordre décroissant
• si le tableau passé en argument contient des entiers tous identiques

Algorithmique (Première) - Autres

n°866
En utilisant une recherche dichotomique, combien faut-il de comparaisons pour trouver une valeur dans un tableau trié de 1000 nombres ?

• 3
• 10
• 1000
• 1024

Algorithmique (Première) - Autres

n°867
Quelle est la valeur de c à la fin de l'exécution du code suivant :

L = [1,2,3,4,1,2,3,4,0,2]  
c = 0  
for k in L:  
    if k == L[1]:  
        c = c+1  

• 0
• 2
• 3
• 10

Algorithmique (Première) - Autres

n°868
La fonction suivante doit calculer le produit de tous les éléments de la liste passée en paramètre. Avec quelles expressions doit-on la compléter pour que cette fonction soit correcte ?

def produit (L):
    p = ...
    for elt in L:
        ........
    return p

• 1 puis p = p * elt
• 0 puis p = p * elt
• 1 puis p = elt
• 0 puis p = elt

Algorithmique (Première) - Autres

n°869
On définit une fonction de calcul de la moyenne d'une liste de nombres :

def moyenne(L):  
    s = 0  
    n = len(L)  
    for x in L:  
        s = s + x  
    return s/n  

Combien cette fonction utilise-t-elle d'additions et de divisions pour calculer la moyenne d'une liste de 7 nombres ?

• 7
• 8
• 9
• 10

Algorithmique (Première) - Autres

n°870
Quelle est la valeur du couple (s,i) à la fin de l'exécution du script suivant ?

s = 0  
i = 1  
while i < 5:  
    s = s + i  
    i = i + 1  

• (4, 5)
• (10, 4)
• (10, 5)
• (15, 5)

Algorithmique (Première) - Autres

n°907
Quelle est la valeur de c à la fin de l'exécution du code suivant :

L = [1,2,3,4,1,2,3,4,0,2]   
c = 0   
for k in L:   
    if k == L[1]:   
        c = c+1   

• 0
• 2
• 3
• 10

Algorithmique (Première) - Autres

n°908
Que renvoie la fonction suivante quand on l'appelle avec un nombre entier et une liste d'entiers ?

def mystere(n,L):  
    for x in L:  
        if n == x:  
            return True  
    return False  

• une valeur booléenne indiquant si le nombre n est présent au moins une fois dans la liste L
• une valeur booléenne indiquant si le nombre n est présent plusieurs fois dans la liste L
• une valeur booléenne indiquant si le nombre n est le plus grand de la liste L
• une valeur booléenne indiquant si le nombre n est le plus petit de la liste L

Algorithmique (Première) - Autres

n°909
La fonction mystere suivante prend en argument un tableau d'entiers.

def mystere(t):   
    for i in range(len(t) - 1):   
        if t[i] + 1 != t[i+1]:   
            return False   
    return True   

À quelle condition la valeur renvoyée par la fonction est-elle True ?

• si le tableau passé en argument est une suite d'entiers consécutifs
• si le tableau passé en argument est trié en ordre croissant
• si le tableau passé en argument est trié en ordre décroissant
• si le tableau passé en argument contient des entiers tous identiques

Algorithmique (Première) - Autres

n°910
On exécute le script suivant :

def recherche(liste):   
    valeur_1 = liste[0]  
    valeur_2 = liste[0]   
    for item in liste:   
        if item < valeur_1:   
            valeur_1 = item   
        elif item > valeur_2:   
            valeur_2 = item   
        else:   
            pass   
    return (valeur_1, valeur_2)  

liste = [48, 17, 25 , 9, 34, 12, -5, 89, 54, 12, 78, 8, 155, -85]  

Que va renvoyer l'appel recherche(liste) ?

• (-85, 155)
• [-85, 155]
• (155, -85)
• (-85; 155)

Algorithmique (Première) - Autres

n°911
Un algorithme de recherche dichotomique dans une liste triée de taille \(n\) nécessite, dans le pire des cas, exactement \(k\) comparaisons.
Combien cet algorithme va-t-il utiliser, dans le pire des cas, de comparaisons sur une liste de taille \(2n\) ?

• \(k\)
• \(k + 1\)
• \(2k\)
• \(2k + 1\)

Algorithmique (Première) - Autres

n°912
On considère la fonction suivante :

def f(x,L):  
    i = 0  
    j = len(L)-1  
    while i < j:  
        k = (i+j)//2  
        if x <= L[k]:  
            j = k  
        else:  
            i = k + 1  
    return i  

Cette fonction implémente :

• le tri par insertion
• le tri par sélection
• la recherche dichotomique
• la recherche du plus proche voisin

Algorithmique (Première) - Autres

n°949
On considère le code incomplet suivant qui recherche le maximum dans une liste.

liste = [5,12,15,3,15,17,29,1]  
iMax = 0  
for i in range(1,len(liste)):  
    ............  
    iMax = i  
print (liste[iMax])  

Par quoi faut-il remplacer la ligne pointillée ?

• if i > iMax:
• if liste[i] > liste[iMax]:
• if liste[i] > iMax:
• if i > liste[iMax]:

Algorithmique (Première) - Autres

n°950
On conçoit un algorithme permettant de déterminer la valeur maximale parmi une liste quelconque de valeurs comparables.
Pour une liste de 100 valeurs, le nombre minimal de comparaisons que doit effectuer cet algorithme est :

• 7
• 99
• 200
• 10000

Algorithmique (Première) - Autres

n°951
Quelle est la valeur de element à la fin de l'exécution du code suivant :

L = [1,2,3,4,1,2,3,4,0,2]  
element = L[0]  
for k in L:  
    if k > element:  
        element = k  

• 0
• 1
• 4
• 10

Algorithmique (Première) - Autres

n°952
Un algorithme de recherche dichotomique dans une liste triée de taille \(n\) nécessite, dans le pire des cas, exactement \(k\) comparaisons.
Combien cet algorithme va-t-il utiliser, dans le pire des cas, de comparaisons sur une liste de taille \(2n\) ?

• \(k\)
• \(k + 1\)
• \(2k\)
• \(2k + 1\)

Algorithmique (Première) - Autres

n°953
La fonction suivante doit calculer la moyenne d’un tableau de nombres, passé en paramètre. Avec quelles expressions faut-il remplacer les points de suspension pour que la fonction soit correcte ?

def moyenne(tableau):  
    total = ...  
    for valeur in tableau:  
        total = total + valeur  
    return total / ...  

• 1 et (len(tableau) + 1)
• 1 et len(tableau)
• 0 et (len(tableau) + 1)
• 0 et len(tableau)

Algorithmique (Première) - Autres

n°954
On considère le code suivant, où n désigne un entier au moins égal à 2.

p = 1  
while p < n:  
    p = 2*p  

Quel argument permet d'affirmer que son exécution termine à coup sûr ?

• p est une puissance de 2
• toute boucle while termine
• les valeurs successives de p constituent une suite d'entiers positifs strictement croissante
• les valeurs successives de n – p constituent une suite d'entiers positifs strictement décroissante

Algorithmique (Première) - Autres

n°993
L'algorithme suivant permet de calculer la somme des N premiers entiers, où N est un nombre entier donné :

i =0
somme = 0
while i < N :
    i = i +1
    somme = somme + i

Un invariant de boucle de cet algorithme est le suivant :

• somme = 0 + 1 + 2 + ... + i et i < N
• somme = 0 + 1 + 2 + ... + N et i < N
• somme = 0 + 1 + 2 + ... + i et i < N+1
• somme = 0 + 1 + 2 + ... + N et i < N+1

Algorithmique (Première) - Autres

n°994
On exécute le script suivant :

for i in range(n):
    for j in range(i):
        print('NSI')

Combien de fois le mot NSI est-il affiché ?

• \(n^{2}\)
• \({(n + 1)}^{2}\)
• \(1 + 2 + \cdots + (n - 1)\)
• \(1 + 2 + \cdots + (n - 1) + n\)

Algorithmique (Première) - Autres

n°995
Quel code parmi les quatre proposés ci-dessous s'exécute-t-il en un temps linéaire en \(n\) (c'est-à-dire avec un temps d'exécution majoré par \(A \times n + B\) où \(A\) et \(B\) sont deux constantes) ?

• for i in range(n//2):
      for j in range(i+1,n):
          print('hello')
  

• for i in range(n):
      print('hello')
  

• L = [ i+j for i in range(n) for j in range(n) ]
  for x in L:
      print('hello')
  

• for i in range(n//2):
      for j in range(n//2):
          print('hello')
  

Algorithmique (Première) - Autres

n°996
On considère le code suivant, où n désigne un entier au moins égal à 2.

p = 1
while p < n:
    p = 2*p

Quel argument permet d'affirmer que son exécution termine à coup sûr ?

• p est une puissance de 2
• toute boucle while termine
• les valeurs successives de p constituent une suite d'entiers positifs strictement croissante
• les valeurs successives de n – p constituent une suite d'entiers positifs strictement décroissante

Algorithmique (Première) - Autres

n°997
Soit \(T\) le temps nécessaire pour trier, à l'aide de l'algorithme du tri par insertion, une liste de 1000 nombres entiers. Quel est l'ordre de grandeur du temps nécessaire, avec le même algorithme, pour trier une liste de 10 000 entiers, c'est-à-dire une liste dix fois plus grande ?

• à peu près le même temps \(T\)
• environ \(10 \times T\)
• environ \(100 \times T\)
• environ \(T^{2}\)

Algorithmique (Première) - Autres

n°998
À quelle catégorie appartient l’algorithme des k plus proches voisins ?

• algorithmes de tri
• algorithmes gloutons
• algorithmes de recherche de chemins
• algorithmes de classification et d’apprentissage

Algorithmique (Première) - Autres

n°1035
On considère le code suivant, où n désigne un entier au moins égal à 2.

p = 1
while p < n:
    p = 2*p

Quel argument permet d'affirmer que son exécution termine à coup sûr ?

• p est une puissance de 2
• toute boucle while termine
• les valeurs successives de p constituent une suite d'entiers positifs strictement croissante
• les valeurs successives de n – p constituent une suite d'entiers positifs strictement décroissante

Algorithmique (Première) - Autres

n°1036
Soit L une liste de \(n\) nombres réels (\(n\) entier naturel non nul). On considère l'algorithme suivant, en langage Python, calculant la moyenne des éléments de L.

M = 0
for k in range(n):
    M = M + L[k]
M = M/n

Si le nombre \(n\) de données double alors le temps d'exécution de ce script :

• reste le même
• double aussi
• est multiplié par \(n\)
• est multiplié par 4

Algorithmique (Première) - Autres

n°1037
On considère la fonction suivante :

def f(T,i):
    indice = i
    m = T[i]
    for k in range(i+1, len(T)):
        if T[k] < m:
            indice = k
            m = T[k]
    return indice

Quelle est la valeur de f([ 7, 3, 1, 8, 19, 9, 3, 5 ], 0) ?

• 1
• 2
• 3
• 4

Algorithmique (Première) - Autres

n°1038
Quel est l’ordre de grandeur du coût du tri par insertion (dans le pire des cas) ?

• l'ordre de grandeur du coût dépend de l'ordinateur utilisé
• linéaire en la taille du tableau à trier
• quadratique en la taille du tableau à trier
• indépendant de la taille du tableau à trier

Algorithmique (Première) - Autres

n°1039
À quelle catégorie appartient l’algorithme des k plus proches voisins ?

• algorithmes de tri
• algorithmes gloutons
• algorithmes de recherche de chemins
• algorithmes de classification et d’apprentissage

Algorithmique (Première) - Autres

n°1040
À quelle catégorie appartient l’algorithme classique de rendu de monnaie ?

• les algorithmes de classification et d'apprentissage
• les algorithmes de tri
• les algorithmes gloutons
• les algorithmes de mariages stables

Algorithmique (Première) - Autres

n°1077
Un algorithme de tri d’une liste d’entiers est implémenté de la façon suivante :

def trier(L) :  
    for i in range(len(L)):  
        indice_min = i  
        for j in range(i+1, len(L)):  
            if L[j] < L[indice_min] :  
                indice_min = j  
            L[i], L[indice_min] = L[indice_min], L[i]  
    return L  

Quelle est l'affirmation exacte ?

• cet algorithme est celui du tri par sélection et il a un coût linéaire en la taille de la liste à trier
• cet algorithme est celui du tri par insertion et il a un coût linéaire en la taille de la liste à trier
• cet algorithme est celui du tri par sélection et il a un coût quadratique en la taille de la liste à trier
• cet algorithme est celui du tri par insertion et il a un coût quadratique en la taille de la liste à trier

Algorithmique (Première) - Autres

n°1078
On considère la fonction suivante :

def comptage(phrase,lettre):  
    i = 0  
    for j in phrase:  
        if j == lettre:  
            i = i+1  
    return i  

Que renvoie l'appel comptage('Vive l’informatique','e') ?

• 0
• 2
• 19
• 'e'

Algorithmique (Première) - Autres

n°1079
Quel code parmi les quatre proposés ci-dessous s'exécute-t-il en un temps linéaire en \(n\) (c'est-à-dire avec un temps d'exécution majoré par \(A \times n + B\) où \(A\) et \(B\) sont deux constantes) ?

• for i in range(n//2):  
      for j in range(i+1,n):  
          print('hello')  
  

• for i in range(n):  
      print('hello')  
  

• L = [ i+j for i in range(n) for j in range(n) ]  
  for x in L:  
      print('hello')  
  

• for i in range(n//2):  
      for j in range(n//2):  
          print('hello')  
  

Algorithmique (Première) - Autres

n°1080
Quelle précondition suppose l'algorithme de recherche dichotomique dans un tableau ?

• que le tableau soit à éléments positifs
• que le tableau soit trié
• que l'élément cherché dans le tableau soit positif
• que l'élément cherché figure effectivement dans le tableau

Algorithmique (Première) - Autres

n°1081
Soit \(T\) le temps nécessaire pour trier, à l'aide de l'algorithme du tri par insertion, une liste de 1000 nombres entiers. Quel est l'ordre de grandeur du temps nécessaire, avec le même algorithme, pour trier une liste de 10 000 entiers, c'est-à-dire une liste dix fois plus grande ?

• à peu près le même temps \(T\)
• environ \(10 \times T\)
• environ \(100 \times T\)
• environ \(T^{2}\)

Algorithmique (Première) - Autres

n°1082
On considère la fonction suivante :

def trouverLettre(phrase,lettre):  
    indexResultat = 0  
    for i in range(len(phrase)):  
        if phrase[i]== lettre:  
            indexResultat=i  
    return indexResultat  

Que renvoie l'appel trouverLettre('Vive l’informatique','e') ?

• 3
• 4
• 18
• 'e'

Algorithmique (Première) - Autres

n°1119
La fonction ci-dessous permet d’effectuer une recherche par dichotomie de l’index m de l’élément x dans un tableau L de valeurs distinctes et triées.

def dicho(x,L):
    g = 0
    d = len(L)-1
    while g <= d:
        m = (g+d)//2
        if L[m] == x:
            return m
        elif L[m] < x:
            g = m+1
        else:
            d = m-1
    return None

Combien de fois la cinquième ligne du code de la fonction (m = (g+d)//2) sera-t-elle exécutée dans l'appel dicho(32, [4, 5, 7, 25, 32, 50, 51, 60]) ?

• 1 fois
• 2 fois
• 3 fois
• 4 fois

Algorithmique (Première) - Autres

n°1120
On définit la fonction f comme suit :

def f(L):
    a = L[0]
    for x in L:
        if x < a:
            a = x
    return a

Quelle est la valeur renvoyée par l'appel f([7, 10.3, -4, 12 ,7 ,2, 0.7, -5, 14, 1.4]) ?

• -5
• 1.4
• 7
• 14

Algorithmique (Première) - Autres

n°1121
À quelle catégorie appartient l’algorithme des k plus proches voisins ?

• algorithmes de tri
• algorithmes gloutons
• algorithmes de recherche de chemins
• algorithmes de classification et d’apprentissage

Algorithmique (Première) - Autres

n°1122
Soit \(T\) le temps nécessaire pour trier, à l'aide de l'algorithme du tri par insertion, une liste de 1000 nombres entiers. Quel est l'ordre de grandeur du temps nécessaire, avec le même algorithme, pour trier une liste de 10 000 entiers, c'est-à-dire une liste dix fois plus grande ?

• à peu près le même temps \(T\)
• environ \(10 \times T\)
• environ \(100 \times T\)
• environ \(T^{2}\)

Algorithmique (Première) - Autres

n°1123
On exécute le code suivant :

tab = [1, 4, 3, 8, 2]
S = 0
for i in range(len(tab)):
    S = S + tab[i]

Que vaut la variable S à la fin de l'exécution ?

• 1
• 8
• 18
• 3.6

Algorithmique (Première) - Autres

n°1124
Un algorithme de calcul de moyenne est implémenté de la façon suivante :

def moyenne(liste) :
    t = 0
    for e in liste :
        t = t + e
        # assertion vraie à cet endroit
    return t/len(liste)

Parmi les propositions suivantes, laquelle reste vraie à la fin de chaque itération de la boucle ?

• e vaut le nombre de passages dans la boucle
• t vaut la somme des éléments visités de la liste
• t vaut la moyenne des éléments visités de la liste
• après k passages dans la boucle la liste contient k termes

Algorithmique (Première) - Autres

n°1161
Lors de l'exécution du code suivant, combien de fois l'opération a = 2*a sera-t-elle effectuée ?

a = 1
cpt = 1
while cpt < 8:
    a = 2*a
    cpt = cpt+1

• 0
• 1
• 7
• 8

Algorithmique (Première) - Autres

n°1162
Qu'affiche le programme suivant :

a = 3
b = 4
if a > b and a == 3:
    print('vert')
if a > b and b == 4:
    print('rouge')
if a == 4 or b > a:
    print('bleu')
if a == 3 or a < b:
    print('jaune')

• vert
  rouge
  
• bleu
  jaune
  
• bleu
• vert
  jaune
  

Algorithmique (Première) - Autres

n°1163
\(a\) et \(m\) étant deux entiers supérieurs à 1, la fonction suivante renvoie \(a^{m}\).

def puissance(a,m):
    p = 1
    n = 0
    while n < m:
        #
        p = p * a
        n = n + 1
    return p

Quelle est l'égalité qui est vérifiée à chaque passage par la ligne marquée # ?

• \(p = a^{n - 1}\)
• \(p = a^{n}\)
• \(p = a^{n + 1}\)
• \(p = a^{m}\)

Algorithmique (Première) - Autres

n°1164
On définit :

def traite(chaine,a):
    nouvelle_chaine = ''
    for k in range(len(chaine)):
        if chaine[k] != a:
            nouvelle_chaine = nouvelle_chaine + chaine[k]
    return nouvelle_chaine

Quelle est la valeur renvoyée par l'appel traite('histoire','i') ?

• 'hstore'
• 'ii'
• 'histoire'
• ''

Algorithmique (Première) - Autres

n°1165
Quelle est la valeur du couple (s,i) à la fin de l'exécution du script suivant ?

s = 0
i = 1
while i < 5:
    s = s + i
    i = i + 1

• (4, 5)
• (10, 4)
• (10, 5)
• (15, 5)

Algorithmique (Première) - Autres

n°1166
Quelle valeur permet de compléter l’affirmation suivante : « Le nombre d’opérations nécessaires pour rechercher un élément séquentiellement dans un tableau de longueur \(n\) est de l’ordre de … » ?

• 1
• \(n\)
• \(n^{2}\)
• \(n^{3}\)

Algorithmique (Première) - Autres

n°1203
Quelle est la complexité du tri par sélection ?

• inconnue
• linéaire
• quadratique
• exponentielle

Algorithmique (Première) - Autres

n°1204
À quelle catégorie appartient l’algorithme classique de rendu de monnaie ?

• les algorithmes de classification et d'apprentissage
• les algorithmes de tri
• les algorithmes gloutons
• les algorithmes de mariages stables

Algorithmique (Première) - Autres

n°1205
On considère la fonction suivante :

def comptage(phrase,lettre):
    i = 0
    for j in phrase:
        if j == lettre:
            i = i+1
    return i

Que renvoie l'appel comptage('Vive l’informatique','e') ?

• 0
• 2
• 19
• 'e'

Algorithmique (Première) - Autres

n°1206
Pour pouvoir utiliser un algorithme de recherche par dichotomie dans une liste, quelle précondition doit être vraie ?

• la liste doit être triée
• la liste ne doit pas comporter de doublons
• la liste doit comporter uniquement des entiers positifs
• la liste doit être de longueur inférieure à 1024

Algorithmique (Première) - Autres

n°1207
Lors de l'exécution du code suivant, combien de fois l'opération a = 2*a sera-t-elle effectuée ?

a = 1
cpt = 1
while cpt < 8:
    a = 2*a
    cpt = cpt+1

• 0
• 1
• 7
• 8

Algorithmique (Première) - Autres

n°1244
On considère le code incomplet suivant qui recherche le maximum dans une liste.
{.quiz}\nliste = [5,12,15,3,15,17,29,1] iMax = 0 for i in range(1,len(liste)): ............ iMax = i print (liste[iMax])\n Par quoi faut-il remplacer la ligne pointillée ?

• if i > iMax:
  

• if liste[i] > liste[iMax]:
  

• if liste[i] > iMax:
  

• if i > liste[iMax]:
  

Algorithmique (Première) - Autres

n°1245
Un algorithme de recherche dichotomique sur un tableau trié de mille entiers s'exécute en 50 millisecondes.
Quelle est la durée approximative de son exécution sur un tableau trié d'un million d'entiers ?

• la même durée : environ 50 millisecondes
• une durée environ deux fois plus longue : environ 100 millisecondes
• une durée environ mille fois plus longue : environ 50 secondes
• une durée qui dépasserait l'année, car la complexité de l'algorithme est exponentielle

Algorithmique (Première) - Autres

n°1246
On considère le code suivant de recherche d'une valeur dans une liste :

def search(x, y):
    # x est la valeur à chercher
    # y est une liste de valeurs
    for i in range(len(y)):
        if x == y[i]:
            return i
    return None

Quel est le coût de cet algorithme ?

• constant
• logarithmique
• linéaire
• quadratique

Algorithmique (Première) - Autres

n°1247
On considère la fonction suivante :
{.quiz}\ndef trouverLettre(phrase,lettre): indexResultat = 0 for i in range(len(phrase)): if phrase[i]== lettre: indexResultat = i return indexResultat\n Que renvoie l'appel trouverLettre('Vive l’informatique','e') ?

• 3
• 4
• 18
• 'e'

Algorithmique (Première) - Autres

n°1248
On exécute le script suivant :

liste = [17, 12, 5, 18, 2, 7, 9, 15, 14, 20]
somme = 0
i = 0
while i < len(liste):
    somme = somme + liste[i]
    i = i + 1
resultat = somme / len(liste)

Quelle affirmation est fausse parmi les suivantes ?

• le corps de la boucle a été exécuté 10 fois
• à la fin de l'exécution la valeur de i est 9
• resultat contient la moyenne des éléments de liste
• len est une fonction

Algorithmique (Première) - Autres

n°1249
Pour pouvoir utiliser un algorithme de recherche par dichotomie dans une liste, quelle précondition doit être vraie ?

• la liste doit être triée
• la liste ne doit pas comporter de doublons
• la liste doit comporter uniquement des entiers positifs
• la liste doit être de longueur inférieure à 1024

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°1296
On considère la fonction suivante :

def mystere(tab1, tab2):  
    '''reçoit deux tableaux de même longueur'  
    for i in range(len(tab1)):  
        if tab1[i] != tab2[i]:  
            return False  
    return True  

Que renvoie la fonction si l'appel est le suivant:

mystere([12, 5, 18, 4],[12, 5, 18, 4])  

• 3
• faux
• True
• False

Algorithmique (Première) - Tri par insertion/sélection

n°1297
On considère un algorithme permettant de trier un tableau d'entiers par ordre croissant :
A quel type tri correspond l'invariant de boucle ci-dessous :
tous les éléments d'indices 0 à i-1 sont déjà triés,
tous les éléments d'indices i à n sont de valeurs supérieures à ceux de la partie triée.

• tri par fusion
• tri par sélection
• tri par insertion
• tri rapide

Algorithmique (Première) - Tri par insertion/sélection

n°1298
Invariant d'un algorithme de tri par sélection :
On considère un algorithme de tri par sélection, dans lequel la fonction:

echanger(tab[i], tab[j])  

effectue l'échange des ième et jième valeurs du tableau tab.

nom: tri\_sélection  
paramètre: tab, tableau de n entiers, n>=2  
Traitement:  
pour i allant de 1 à n-1:  
 pour j allant de i+1 à n:  
 si tab[j] < tab[i]:  
 echanger(tab[i], tab[j])  
renvoyer tab  

Question: quel est l'invariant de boucle qui correspond précisément à cet algorithme ?

• Tous les éléments d'indice supérieur ou égal à i sont triés par ordre croissante
• Tous les éléments d'indice compris entre 0 et i sont triés et les éléments d'indice supérieurs ou égal à i leurs sont tous supérieurs
• Tous les éléments d'indice supérieur ou égal à i sont non triés
• Tous les éléments d'indice compris entre 0 et i sont triés, on ne peut rien dire sur les éléments d'indice supérieur ou égal à i

Algorithmique (Première) - Tri par insertion/sélection

n°1299
Algorithme de tri
On considère un algorithme de tri dans lequel la fonction:

echanger(tab[i], tab[j])  

effectue l'échange les ième et jième valeurs du tableau tab.

nom: tri\_mystere  
paramètre: tab, tableau de n entiers, non trié, non vide  
Traitement:  
pour i allant de 1 à n-1:  
 pour j allant de i+1 à n:  
 si tab[j] < tab[i]:  
 echanger(tab[i], tab[j])  
renvoyer tab  

Question: quel est le type de tri qui correspond à cet algorithme ?

• tri par sélection
• tri fusion
• tri rapide
• tri par insertion

Algorithmique (Première) - Tri par insertion/sélection

n°1300
Algorithme de tri
On considère un algorithme de tri dans lequel la fonction:

echanger(tab[i], tab[j])  

effectue l'échange les ième et jième valeurs du tableau tab.

nom: tri\_mystere  
paramètre: tab, tableau de n entiers, non trié, non vide  
Traitement:  
pour i allant de 1 à n-1:  
 pour j allant de i+1 à n:  
 si tab[j] < tab[i]:  
 echanger(tab[i], tab[j])  
renvoyer tab  

Question: quel est le type de tri qui correspond à cet algorithme ?

• tri par sélection
• tri fusion
• tri rapide
• tri par insertion

Algorithmique (Première) - Tri par insertion/sélection

n°1301
Invariant d'un algorithme de tri par insertion :
On considère un algorithme de tri par insertion, dans lequel la fonction:

echanger(tab[i], tab[j])  

effectue l'échange les ième et jième valeurs du tableau tab.

nom: tri\_insertion  
paramètre: tab, tableau de n entiers, n >= 2  
Traitement:  
pour i allant de 2 à n:  
 j = i  
 tant que j > 1 et tab[j-1] > tab[j]:  
 echanger(tab[j-1], tab[j])  
 j = j-1  
renvoyer tab  

Question: quel est l'invariant de boucle qui correspond précisément à cet algorithme ?

• Tous les éléments d'indice compris entre 0 et i sont triés et les éléments d'indice supérieurs ou égal à i leurs sont tous supérieurs
• Tous les éléments d'indice supérieur ou égal à i sont triés par ordre croissant
• Tous les éléments d'indice compris entre 0 et i sont triés, on ne peut rien dire sur les éléments d'indice supérieur ou égal à i
• Tous les éléments d'indice supérieur ou égal à i sont non triés par ordre croissants

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°1343
Quelle est la valeur de X/m à la fin de l'exécution du code suivant :

L = [1,2,3,4,1,2,3,4,0,2]
X = 0
m = 0
for k in L:
    X = X + k
    m = m + 1

• 2
• 2.2
• 10
• 22

Algorithmique (Première) - Recherche Dichotomique

n°1357
La recherche dichotomique est un algorithme rapide qui permet de trouver ou non la présence d’un élément dans un tableau. Mais, pour l’utiliser, une contrainte est indispensable, laquelle ?

• le tableau ne contient que des nombres positifs
• la longueur du tableau est une puissance de 2
• le tableau est trié en ordre croissant
• le tableau ne contient pas la valeur 0

Algorithmique (Première) - Algorithme KNN

n°1358
Une seule des affirmations suivantes est vraie :

• L'algorithme des k plus proches voisins a pour but de déterminer les k plus proches voisins d'une observation dans un ensemble de données.
• L'algorithme des k plus proches voisins a pour but de déterminer la classe d'une observation à partir des classes de ses k plus proches voisins.
• L'algorithme des k plus proches voisins a pour but de déterminer dans un ensemble de données le sous-ensemble à k éléments qui sont les plus proches les uns des autres.
• L'algorithme des k plus proches voisins a pour but de déterminer les éléments d'un ensemble de données appartenant à une même classe.

Algorithmique (Première) - Algorithme KNN

n°1380
On dispose d’une table de données de villes européennes. On utilise ensuite l’algorithme des k-plus proches voisins pour compléter automatiquement cette base avec de nouvelles villes.
| Ville | Pays | Distance jusqu’à Davos |
| --- | --- | --- |
| Berne | Suisse | 180 km |
| Innsbruck | Autriche | 130 km |
| Milan | Italie | 150 km |
| Munich | Allemagne | 200 km |
| Stuttgart | Allemagne | 225 km |
| Turin | Italie | 250 km |
| Zurich | Suisse | 115 km |
En appliquant l’algorithme des 4 plus proches voisins, quel sera le pays prédit pour la ville de Davos ?

• Allemagne
• Autriche
• Italie
• Suisse

Algorithmique (Première) - Algorithmes Gloutons

n°1381
Parmi les phrases suivantes, laquelle est vraie ?

• un algorithme glouton fournit toujours une solution optimale
• un algorithme glouton est généralement moins complexe que les autres méthodes d’optimisation
• un algorithme glouton étudie tous les cas possibles pour déterminer l’optimal
• un algorithme glouton peut revenir en arrière en cas de blocage

Algorithmique (Première) - Autres

n°1520
Combien vaut la variable x à la fin de cet algorigramme si a=26 b=29 et c=26 ?

• x = 26
• x = 29
• x = 25
• x = 28

Algorithmique (Première) - Algorithmes Gloutons

n°1582
Sac à dos
Un sherpa doit traverser la montagne pour vendre des marchandises dans le village voisin. Il ne peut transporter plus de 20kg dans son sac à dos et il dispose de 5 objets de poids différents et de valeurs différentes.
Voici cette liste d'objets sous forme de tuple (nom de l'objet , valeurs en euros , poids en kg)

Objets=[('A',10,9),('B',7,12),('C',1,2),('D',3,7),('E',2,5)]

Il se demande quels objets choisir pour transporter la valeur totale maximale dans son sac tout en ne dépassant pas 20 kg.
Quels objets doit-il mettre dans son sac s'il applique un algorithme glouton dans la résolution de ce problème ?

• Objet 'A' puis objet 'D' puis objet 'C'
• Objet 'B' puis objet 'D'
• Objet 'B' puis objet 'A' puis objet 'D'
• Objet 'B' puis objet 'D' puis objet 'E' puis objet 'C'

Algorithmique (Première) - Recherche Dichotomique

n°1585
Dans une recherche par dichotomie, combien de comparaisons faut-il faire pour trouver une valeur dans un tableau trié de 1000 nombres ?

• 3
• 10
• 1000
• 1024

Algorithmique (Première) - Autres

n°1610
PAR QUEL MOYEN USUEL PEUT-ON DÉMONTRER LA TERMINAISON D’UNE BOUCLE ?

• une assertion
• un invariant
• un variant
• la complexité

Algorithmique (Première) - Tri par insertion/sélection

n°1611
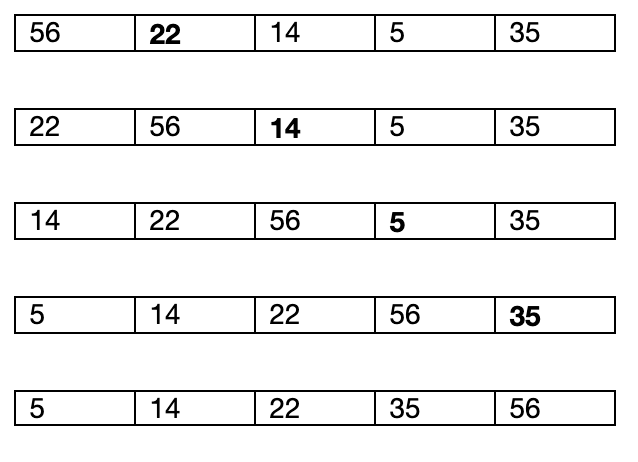
SOIT UN TABLEAU À TRIER: [56, 22, 14, 5, 35]. QUEL ALGORITHME A TRIÉ CE TABLEAU ?
Les étapes de tri sont les suivantes, l'élément trié est en gras:

• algorithme par sélection
• algorithme par insertion
• algorithme glouton
• algorithme dichotomique

Algorithmique (Première) - Autres

n°1612
QCM diagnostic sur l'algorithmique
Quelle est la particularité essentielle d'une boucle 'tant que' ?

• On sait à l'avance combien de tour de boucles vont être effectués
• Il est possible de faire une infinité de tours
• Au moins un tour de boucle est effectué

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°1613
QCM diagnostic sur l'algorithmique
Pour trouver la valeur maximale d'un tableau composé de n nombre entiers :

• Il faut parcourir le tableau n fois
• Il faut parcourir le tableau partiellement
• Il faut parcourir le tableau en totalité

Algorithmique (Première) - Parcours séquentiel d'un tableau

n°1614
QCM diagnostic sur l'algorithmique
Pour trouver la valeur moyenne d'un tableau composé de n nombre entiers :

• Il faut parcourir le tableau n fois
• Il faut parcourir le tableau en totalité
• Il faut parcourir le tableau partiellement

Algorithmique (Première) - Recherche Dichotomique

n°1616
Avec l’algorithme de recherche dichotomique, on recherche un nom dans un annuaire de 30 000 noms qui sont rangés dans l’ordre alphabétique. Quel est le nombre maximal d'étapes pour trouver ce nom ?

• 11
• 13
• 15
• 17

Algorithmique (Première) - Recherche Dichotomique

n°1617
Une liste contient 65 536 nombres entiers triés dans l'ordre croissant. Quel est le nombre maximal d'étapes pour trouver un nombre de cette liste en utilisant un algorithme de recherche dichotomique ?

• 17
• 16
• 15
• 14

Algorithmique (Première) - Algorithmes Gloutons

n°1619
Sac à dos
Un sherpa doit traverser la montagne pour vendre des marchandises dans le village voisin. Il ne peut transporter plus de 20kg dans son sac à dos et il dispose de 5 objets de poids différents et de valeurs différentes
Voici cette liste d'objets sous forme de tuple (nom de l'objet , valeurs en euros , poids en kg)

Objets=[('A',2,5),('B',10,9),('C',3,7),('D',1,2),('E',7,12)]

Il se demande quels objets choisir pour transporter la valeur totale maximale dans son sac tout en ne dépassant pas 20 kg.
Quels objets doit-il mettre dans son sac s'il applique un algorithme glouton dans la résolution de ce problème ?

• B puis D puis C
• B puis E puis D
• E puis C
• je ne sais pas

Algorithmique (Première) - Recherche Dichotomique

n°1841
Avec un algorithme de recherche dichotomique, combien d'étapes sont nécessaires pour déterminer que 35 est présent dans
la liste suivante :

[1, 7, 12, 16, 18, 20, 24, 28, 35, 43, 69]?

• 1
• 2
• 9
• 11

Algorithmique (Première) - Recherche Dichotomique

n°1842
Avec un algorithme de recherche dichotomique, combien d'étapes sont nécessaires pour déterminer que 45 n'est pas présent dans
la liste suivante :

[1, 7, 12, 16, 18, 20, 24, 28, 35, 43, 69]?

• 2
• 3
• 4
• 5

Algorithmique (Première) - Recherche Dichotomique

n°1843
A l'aide de la fonction suivante, on souhaite rechercher une valeur dans la liste [3, 3, 5, 6, 8, 11, 13, 14, 14, 17, 19, 21, 23]

def recherche_dichotomique(tab, val):
    gauche = 0
    droite = len(tab) - 1
    while gauche <= droite:
        milieu = (gauche + droite) // 2
        print(tab[milieu])
        if tab[milieu] == val:
            # on a trouvé val dans le tableau à la position milieu
            return milieu
        elif tab[milieu] > val:
            # on cherche entre gauche et milieu - 1
            droite = milieu - 1
        else: # on a tab[milieu] < val
            # on cherche entre milieu + 1 et droite
            gauche = milieu + 1
        # on est sorti de la boucle sans trouver val
    return -1

Combien de comparaisons sont nécessaires pour retrouver la valeur 14 ?

• 2
• 3
• 4
• impossible

Algorithmique (Première) - Algorithmes Gloutons

n°1896
Principe
Pour rendre la monnaie, il est possible d'utiliser un algorithme glouton.
Une seule des affirmations suivantes est vraie :

• Avec un algorithme glouton, on rend la monnaie en commençant toujours par la pièce ayant la plus grande valeur possible et en procédant ensuite par valeurs décroissantes.
• Avec un algorithme glouton, on rend la monnaie en commençant toujours par la pièce de plus petite valeur afin de maximiser le nombre de pièces rendues.
• Quel que soit le type de pièces dans un pays donné, un algorithme glouton donne toujours la monnaie de manière optimale.
• Un algorithme glouton procède en testant toutes les combinaisons possibles de pièces afin de trouver le rendu optimal.