Enonce

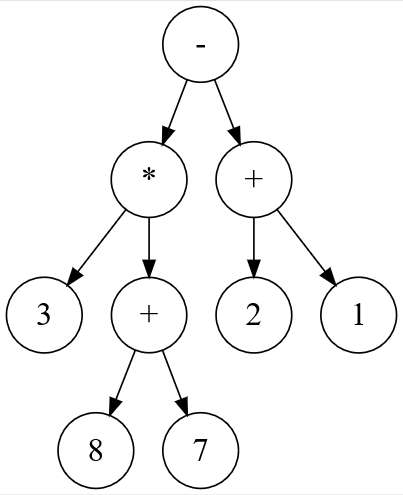
Une expression arithmétique ne comportant que les quatre opérations +, −, ×, ÷ peut être représentée sous forme d’arbre binaire. Les nœuds internes sont des opérateurs et les feuilles sont des nombres. Dans un tel arbre, la disposition des nœuds joue le rôle des parenthèses que nous connaissons bien.

En parcourant en profondeur infixe l’arbre binaire ci-dessus, on retrouve l’expression notée habituellement :

\[(3 \times (8 + 7)) − (2 + 1)\]

La classe Noeud ci-après permet d’implémenter une structure d’arbre binaire.

Compléter la fonction récursive expression_infixe qui prend en paramètre un objet de la classe Noeud et qui renvoie l’expression arithmétique représentée par l’arbre binaire passé en paramètre, sous forme d’une chaîne de caractères contenant des parenthèses.

Résultat attendu avec l’arbre ci-dessus :

>>> e = Noeud(Noeud(Noeud(None, 3, None), '*', Noeud(Noeud(None, 8, None),
'+', Noeud(None, 7, None))), '-', Noeud(Noeud(None, 2, None), '+',
Noeud(None, 1, None)))

>>> expression_infixe(e)
'((3*(8+7))-(2+1))'

class Noeud:
    '''
    classe implémentant un noeud d'arbre binaire
    '''

    def __init__(self, g, v, d):
        '''
        un objet Noeud possède 3 attributs :
        - gauche : le sous-arbre gauche,
        - valeur : la valeur de l'étiquette,
        - droit : le sous-arbre droit.
        '''
        self.gauche = g
        self.valeur = v
        self.droit = d

    def __str__(self):
        '''
        renvoie la représentation du noeud en chaine de caractères
        '''
        return str(self.valeur)

    def est_une_feuille(self):
        '''
        renvoie True si et seulement si le noeud est une feuille
        '''
        return self.gauche is None and self.droit is None


def expression_infixe(e):
    s = ...
    if e.gauche is not None:
        s = '(' + s + expression_infixe(...)
    s = s + ...
    if ... is not None:
        s = s + ... + ...
    return s