Enonce

On considère la classe ABR, dont le constructeur est le suivant :

class ABR:
    def __init__(self, g0, v0, d0):
        self.gauche = g0
        self.cle = v0
        self.droit = d0

    def __repr__(self):
        if self is None:
            return ''
        else:
            return '(' + (self.gauche).__repr__() + ',' + str(self.cle) + ',' +(self.droit).__repr__() + ')'

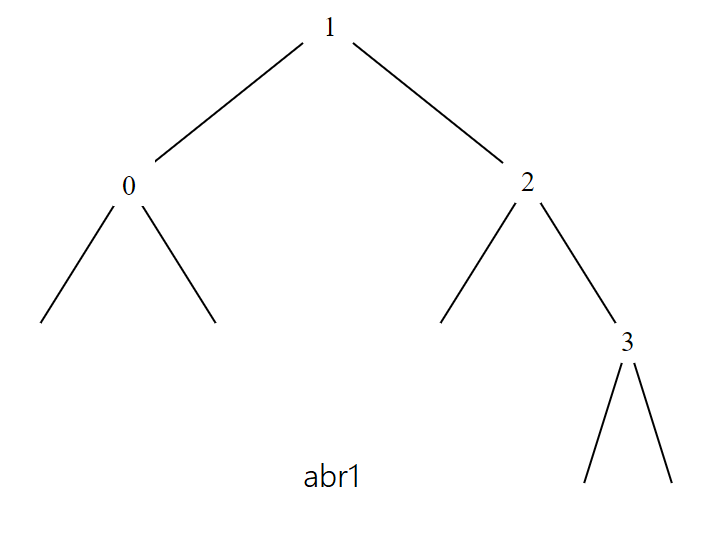
Ainsi, l’arbre binaire de recherche abr1 ci- contre est créé par le code python ci- dessous

n0 = ABR(None, 0, None)
n3 = ABR(None, 3, None)
n2 = ABR(None, 2, n3)
n3 = ABR(n0, 1, n2)

Dans tout le code, None correspondra à un arbre vide.

La classe ABR dispose aussi d’une méthode de représentation (__repr__ ), qui affiche entre parenthèses le contenu du sous arbre gauche, puis la clé de l’arbre, et enfin le contenu du sous arbre droit. Elle s’utilise en console de la manière suivante :

>>> abr1
((None,0,None),1,(None,2,(None,3,None)))

Écrire une fonction récursive ajoute(cle, a) qui prend en paramètres une clé cle et un arbre binaire de recherche a , et qui renvoie un arbre binaire de recherche dans lequel cle a été insérée. Dans le cas où cle est déjà présente dans a, la fonction renvoie l’arbre a inchangé.

Résultats à obtenir :

>>> a = ajoute(4, abr1)
>>> a
((None,0,None),1,(None,2,(None,3,(None,4,None))))

>>> ajoute(-5, abr1)
(((None,-5,None),0,None),1,(None,2,(None,3,None)))

>>> ajoute(2, abr1)
((None,0,None),1,(None,2,(None,3,None)))